

Une approche sensorielle et expérimentale du son
partie I
Sons graves, sons aigus: hauteur et fréquence
Alain Boudet
Dr en Sciences Physiques
Résumé: Cet article est le premier de la série consacrée à la compréhension des caractéristiques physiques du son. Par l'expérience sensorielle, à travers des exemples familiers et grâce à des fichiers sonores inclus, nous découvrons les qualités physiques et musicales des sons, en commençant dans cette première partie par leur hauteur. L'expression vocale peut profiter de ces prises de conscience et je propose quelques exercices vocaux d'applications
 Partie
I:
Sons graves, sons aigus: hauteur et fréquence
Partie
I:
Sons graves, sons aigus: hauteur et fréquence
Partie II: Sons forts, sons faibles: intensité et nuances
Partie III: Couleurs sonores: timbre et harmoniques
Contenu de la partie I
Comment vous parler du son? Le son a tellement de facettes que je lui consacre plusieurs articles. Et vous, si je vous dis "son", qu'est-ce que cela vous évoque?
Quelles images, quelles sensations, quels sentiments?
La musique, les CD, les bruits de la nature, les bruits de la vie quotidienne?
Votre voix?
L'article en trois parties qui suit est une invitation à une écoute affinée afin d'apprendre à connaitre les qualités du son par l'expérience sensorielle. Nous allons décrire successivement les 3 qualités physiques principales du son, à savoir la hauteur, l'intensité et le timbre, avec l'approche de l'être sensible que nous sommes tous, complétée par celles du physicien, de l'acousticien et du musicien.
Les sons font tellement partie de notre univers qu'ils nous imprègnent de façon consciente et inconsciente dans les domaines les plus variés de notre vie. Notre oreille est stimulée par les sons de façon quasi-permanente. Pour le meilleur et pour le pire.
Le son ne touche pas seulement l'oreille, mais le corps entier et à travers lui, atteint divers niveaux de notre être, physique, émotionnel, mental, spirituel. Selon les personnes ou les circonstances, c'est un aspect ou un autre qui est mis en jeu. Par exemple, s'il survient un fort coup de tonnerre, une personne éprouvera de la peur, et éventuellement la manifestera. Quelqu'un d'autre va rester paisible, comptant le nombre de secondes entre l'éclair et le tonnerre, intéressé par cet aspect informationnel. Le niveau le plus immédiat est peut-être l'émotion que le son ou la musique nous procurent, de plaisir ou de déplaisir, quelquefois d'extase. Un autre phénomène extraordinaire lié au son est la résonance physique qui se produit dans notre corps et comment cette interaction peut harmoniser ou déséquilibrer les circuits énergétiques de notre corps. J'aborderai ces aspects dans d'autres pages (voir Résonances sonores corporelles).
Il y a aussi les sons qu'on émet soi-même. Comment dire l'importance de notre propre voix? A la fois comme instrument de communication, reflet de notre personnalité et de notre richesse, et comme expression de notre désir de chanter. Envie tout à fait naturelle et vivante, présente chez l'enfant dès le plus jeune âge, émergeant de nos élans intimes, à moins que nous ne soyons entravés par des jugements et que nous ayons honte de notre voix.
Le physicien est bien placé pour décrire les caractéristiques du son. Mais détient-il la vérité? L'acousticien a un autre point de vue, qui tient compte de la physiologie et de la psychologie de l'auditeur. Je décrirai également l'approche du musicien, basée sur sa sensibilité et sur un système de notation de la musique occidentale. Mentionnons celle du musicothérapeute, qui s'intéresse à l'aspect équilibrant, nourrissant et guérisseur du son. Ce sont toutes des vérités, qui répondent à des interrogations différentes, s'adressent à des plans différents de la personne humaine. Nous nous aiderons de certains appareillages et logiciels du physicien et de l'acousticien destinés à préciser et illustrer certaines notions. Toutefois, nous laisserons de côté les explications scientifiques théoriques. Bien qu'elles soient utiles et passionnantes, elles ne prennent sens que si elles reposent sur du vécu et perçu.
C'est la recherche de ce ressenti sensoriel qui va nous guider dans notre découverte de la hauteur, de l'intensité et du timbre des sons.
Commençons notre exploration du monde sonore en écoutant les voix humaines, sans jugement, juste pour leurs sonorités multiples. Remarquons la différence entre les voix de femmes et les voix d'hommes par exemple. Pour la plupart d'entre nous, c'est notre expérience première, puisque nous avons écouté la voix de notre mère et celle de notre père, même à l'intérieur de l'utérus maternel. Les femmes ont des voix plus aiguës, et les hommes des voix plus graves. La qualité sonore qui nous permet de faire la distinction entre les sons graves et les sons aigus est leur hauteur.
Les hauteurs de sons sont également très perceptibles lorsque nous les prononçons ou les chantons nous-mêmes. Nous pouvons généralement identifier si nous chantons dans le bas de notre voix ou dans le haut. Toutefois, ce n'est pas toujours le cas car il existe des défauts de perception liés à des causes le plus souvent psychologiques, rarement physiques. Une éducation permet de retrouver une perception juste (voir mon article sur La puissance thérapeutique des sons).
Alors chantons des sons au hasard. Peut-être entonnerez-vous une mélodie. Les mélodies sont composées de notes successives qui sont comme des paliers de sons à différentes hauteurs.
Et si je vous propose de chanter des sons qui montent et descendent de façon continue?
Cela ne vous semble pas naturel? Pourtant dans la nature, le vent nous fournit des mouvements continus du son en hauteur, surtout par jour de tempête, des montées et descentes du son. Nous pouvons l'imiter par la voix (écoutez l'illustration sonore jointe, voir la représentation graphique fig.1).
Pour écouter l'extrait sonore
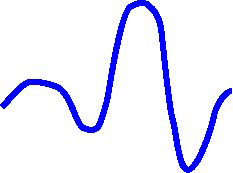
Figure 1. Vagues montantes et descendantes
Peut-être préférez-vous des sons plus mécaniques produits par les machines. Une sirène, une moto qui démarre avec une forte accélération, une débroussailleuse à fil, produisent des sons qui montent et descendent de façon continue.
Avec cette idée des vagues de sons, revenons à la voix humaine. Ne produisons-nous pas habituellement et naturellement des sons montants et descendants? Et oui, et très souvent, mais nous n'y prêtons pas attention. Il s'agit des intonations de nos phrases dans le langage, celles qui différent d'un accent régional à un autre par exemple. Encore plus typiques sont les intonations accompagnant l'expression de nos émotions: "oh", "ah", "ah bon!", "ouah!", ou encore des gémissements, cris, etc.
Les instruments de musique occidentaux sont conçus plutôt pour produire les notes par palier, autrement dit des notes fixes, cependant nombreux sont ceux qui sont capables d'émettre des sons montants et descendants, comme la famille des violons. Le violoncelle sait très bien imiter la voix humaine.
On peut donner une représentation imagée de ces montées et descentes par des graphiques (fig.1). Les sons hauts sont dits aigus et les sons bas sont dits graves (grave comme gravité terrestre).
Depuis longtemps, on sait que les sons sont produits par des vibrations. Ainsi, un son peut faire vibrer des objets autour de nous, les vitres de la fenêtre par exemple. Le technicien du son peut observer que les membranes de ses haut-parleurs vibrent lorsqu'elles émettent des sons. Ces vibrations sont lentes pour les sons graves au point qu'on voit la membrane se gonfler vers l'avant et revenir vers l'arrière de façon répétitive. Les allers et retours deviennent d'autant plus rapides que le son est élevé.
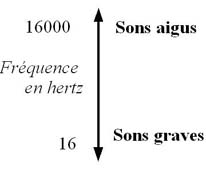
Figure 2. Échelle de fréquence des sons audibles
Grâce à des expériences extrêmement simples, les physiciens ont pu relier la hauteur du son à sa fréquence de vibration (voir mon article Histoire de la notion de fréquence sonore).
Ils mesurent la vitesse de vibration par le nombre d'allers et retours que fait la membrane par seconde, qu'il nomme la fréquence. Elle est mesurée en un nombre par seconde, encore appelé des "périodes par seconde" (abréviation ps) ou hertz (abréviation Hz). Un hertz correspond à 1 vibration par seconde. Un kilohertz (kHz) correspond à 1000 vibrations par seconde et un mégahertz (MHz) à 1 million de vibrations par seconde. L'oreille perçoit les sons sur une échelle de fréquences allant à peu près de 16 hertz (son très grave) à 16 000 hertz (son très aigu). Ces limites d'audibilité ne sont pas strictes et varient en fonction des individus.
Pour nous rendre compte des valeurs des fréquences, écoutons deux sons, l'un grave de 110 Hz, suivi d'un autre aigu, de 3520 Hz, dans cette illustration sonore.
Cependant, il faut faire une distinction entre la hauteur absolue, mesurée par la fréquence, et la perception de la hauteur. Comme le dit E. Leipp, la sensation de hauteur d'un son de fréquence donnée varie avec la hauteur absolue du son, avec son timbre, avec son intensité, avec le contexte musical.
Exercice: Je vous fais entendre un son, celui-ci:
Je vous demande de le chanter avec votre voix.
Puis celui-ci:
Vous pouvez faire la même chose en produisant une note avec un clavier, ou tout autre instrument et le chanter. Si vous n'y arrivez pas, ce n'est pas important. Il ne vous manque que l'entraînement à la justesse de voix, qui passe par la sensation corporelle des sons (voir article Résonances des sons dans le corps).
Les musiciens accordent leurs instruments avant de commencer à jouer de manière à ce qu'ils aient tous le même LA. Or ils s'alignent sur un LA produit par un petit appareil nommé un diapason. Est-ce à dire que ce LA est fixé? Effectivement. Toutefois, la hauteur du LA et des autres notes a longtemps été assez approximative sans que cela pose de problème. Pour le musicien, les hauteurs sont plus relatives qu'absolues. Ce qui importe est l'écart juste entre les notes. Ceci est lié à la notion de gammes et de modes (voir article Gammes et modes musicaux).
Vous êtes peut-être habitués aux notes données par le piano pour lequel un DO est un DO. Et lorsqu'un musicien rencontre un musicien, qu'est-ce qu'ils se disent? Accordons-nous. C'est-à-dire vérifions que nous avons bien le DO à la même hauteur. Mais la définition de la hauteur d'un DO ou d'un LA est arbitraire. Et oui! La notion de hauteur déterminée n'existait même pas en Occident avant le XVIe siècle. Puis la hauteur du LA (et des autres notes) a varié dans le temps et dans l'espace, selon les régions et les pays, selon les époques et selon les instruments. Plus encore, elle pouvait varier d'un bâtiment à l'autre d'une même ville. En Europe, des mesures sur les instruments d'époque montrent pour le LA un étalement de plus de 2 tons. Cependant, on a peu à peu attribué une fréquence fixe aux notes. C'est ce qu'on appelle le diapason. Fixer un diapason national ou international est une idée moderne plus ou moins respectée.
En France le LA3 a été fixé à 435 hertz en 1859, avant d'être détrôné par le LA international. En 1939, la Fédération internationale des associations nationales de standardisation (ancêtre de l'Organisation internationale de normalisation ou ISO) fixe arbitrairement le LA3 à 440 hertz à la température de 20°C. En 1953, la Conférence internationale de Londres l'officialise.
Voir beaucoup plus de détails dans mon article: La hauteur des notes de musique doit-elle être normalisée par un diapason? Les aléas historiques de la fréquence du LA.
Dans les chants, la mélodie se promène par sauts de note en note, contrairement aux chants du vent et de la sirène qui glissent de façon continue. C'est comme si la rampe continue qui permet aux vélos et poussettes de monter la pente, a cédé la place à un escalier composé de marches espacées de façon ordonnée mais pas régulière. Les notes sont comme des paliers, des niveaux de hauteur de son. En musique, l'écart de hauteur entre 2 sons s'appelle un intervalle.
Exercice: Écoutez deux notes successives différentes, qui constituent un intervalle, et amusez-vous à reproduire ces deux notes avec votre voix. Essayez avec celui-ci:
Exercez-vous avec des intervalles variés, en jouant deux touches au hasard sur un clavier par exemple, ou avec un autre instrument. Commencez par les plus simples, avec des touches proches l'une de l'autre.
L'intervalle entre deux touches de piano consécutives s'appelle un demi-ton. Intervalle entre un SI et un DO, par exemple, ou entre une touche noire et la blanche adjacente. Bien évidemment, on peut produire des intervalles qui ne sont ni des demi-tons, ni des tons ou leurs multiples: on peut sauter d'un son à un autre sans s'occuper des notes avec notre voix, ou avec des instruments de musique qui ne produisent pas de notes fixes comme le violon ou certaines flûtes rustiques. Il est possible et tout à fait intéressant d'entendre et de reproduire des intervalles beaucoup plus petits qu'un demi-ton (micro-intervalles).
La musique est faites d'intervalles variés et innombrables. C'est la présence de certains intervalles plutôt que d'autres qui donne à une musique sa couleur orientale, chinoise, indienne ou occidentale par exemple. Car l'assemblage des intervalles produit les modes et des gammes (voir l'article Gammes et modes musicaux).
Toutefois, il est un intervalle que l'on retrouve dans toutes les gammes et dans toutes les cultures, un intervalle universel, c'est l'octave. Qu'est-ce que l'octave? La meilleure façon de vous la définir n'est-elle pas de vous le présenter, de vous le faire écouter?

Figure 3. Deux sauts d'octaves successifs
Exercice: chantez le premier intervalle d'octave entendu ci-dessus. Vous pouvez vous aider en imaginant que vous chantez (si vous la connaissez) la chanson suisse "Là-haut sur la montagne". Ce sont les deux premières notes, l'intervalle entre "là" et "haut".
Cet intervalle est universel parce qu'il est naturel, constitutionnel de notre nature. Il est facile de s'en rendre compte en comparant la voix féminine à la voix masculine. Demandons à un homme de chanter une petite mélodie et à sa compagne de chanter la même chose avec lui. Avec sa voix de femme, elle chantera naturellement plus haut que l'homme: exactement une octave plus haut. Et pourtant, tout en sachant que leurs voix sont différentes, ils auront la sensation de chanter la même chose, d'être ensemble, à l'unisson. Deux sons distants d'une octave, c'est le même son à deux niveaux différents.
En musique, deux sons distants d'une octave portent le même nom. Si le son grave est un DO, le son à l'octave au-dessus sera aussi un DO. Pour les distinguer, on leur attribue un numéro d'ordre qui augmente de 1 en montant: DO1, DO2, DO3, etc.... De même pour toutes les notes: LA3, LA4...
Dans les octaves graves en-dessous du DO1, on trouve, du moins pour la France, DO-1 et DO-2. Car la notation change selon les pays. En Grande Bretagne et aux Etats-Unis, on ne nomme pas les notes LA, SI, DO, RÉ, MI, FA, SOL, mais A, B, C, D, E, F, G. Pour la numérotation des octaves, l'octave de référence, l'octave numéro 1, n'est pas le même. Selon la notation anglaise, le A1 sonne une octave en dessous du LA1 français. Donc le LA3 français est équivalent au A4. En France, on n'utilise pas le zéro, alors qu'on l'utilise dans d'autres pays, et on peut donc trouver aussi la notation DO0 et DO-1 dans des partitions se référant à ces pays.
Pourtant, tous ne suivent pas ces règles. Les logiciels d'édition et de production sonore se réfèrent généralement aux habitudes anglaises et adoptent pour le LA3 la notation A4, qu'ils traduisent en français par LA4. Le même LA peut donc être appelé LA3 si l'on est fidèle à la tradition française ou LA4 s'il est calqué sur l'américain. D'après les concepteurs de ces logiciels, cela évite d'avoir des LA-1 et permet d'avoir un langage cohérent avec des musiciens étrangers.
Dans cet article, je conserve la notation française habituelle du LA3.
Le technicien qui mesure les fréquences de 2 sons distants d'une octave constate que leurs fréquences sont dans un rapport 2. Par exemple, le son grave a une fréquence de 30 hertz et le son aigu de 60 hertz; ou encore 2000 et 4000 hertz. La connaissance de la fréquence des sons fait donc apparaître des chiffres caractéristiques: à l'octave est associé le chiffre 2. L'article Ton et intonation juste rapporte les nombres associés aux autres intervalles dans trois types de gammes majeures. Ainsi pour les LA, on a les mesures suivantes:
| Note | LA-1 | LA1 | LA2 | LA3 | LA4 | LA5 | LA6 |
|---|---|---|---|---|---|---|---|
| Fréquence en hertz | 55 | 110 | 220 | 440 | 880 | 1760 | 3520 |
On sait donc maintenant que l'exemple sonore de la figure 2 montrant l'amplitude des fréquences audibles va d'un LA1 à un LA6, à 5 octaves d'intervalle.
Les musiciens repèrent la hauteur du son par les notes de la gamme. En Occident, les gammes de la musique classique et populaire reposent sur 7 notes de base s'inscrivant à l'intérieur d'une octave et répétées aux autres octaves. En français, ce sont les notes:
DO - RÉ - MI - FA - SOL - LA - SI
Tandis que la hauteur des LA est déterminée en fréquence par la convention internationale, les fréquences des autres notes ne peuvent pas être fixées de façon absolue, car elles dépendent de la gamme dans laquelle elles sont employées, et donc de la culture, de la conception que l'on a de la définition des intervalles, de notre jugement sur la justesse de la voix et en définitive de l'interprétation. Des détails sur les intervalles des gammes sont données dans l'article Ton et intonation juste.
En anglais, on désigne ces notes par A (La) - B (Si) - C (Do, etc.) - D - E - F - G. En allemand, le B désigne un Si bémol, tandis que le Si est désigné par la lettre H.
Dans la gamme chromatique tempérée en usage actuellement, l'octave est partagée en 12 demi-tons équidistants:
DO - DO# ou RÉb - RÉ - RÉ# ou MIb - MI - FA - FA# ou SOLb - SOL - SOL# ou LAb - LA - LA# ou SIb - SI - DO
Pour indiquer les hauteurs sur une partition, le musicien représente les notes sur une portée générale à 11 lignes, divisée en deux portées à 5 lignes, une en clé de Sol et une en clé de FA (figure 4).
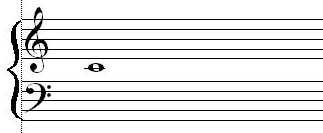
Figure 4. La portée de 11 lignes, avec le DO au milieu, représente l'échelle des hauteurs de notes par degrés
On peut imaginer cette portée comme une projection graphique de l'échelle sonore: les sons graves sont inscrits dans le bas et les sons aigus dans le haut sur une étendue d'environ 3 octaves, sans parler de ceux qu'on peut ajouter en bas et en haut. Le temps se déroule de gauche à droite.
Enfin, je signale qu'il existe une correspondance entre l'échelle verticale des sons et le corps. Les sons résonnent dans le corps et ces résonances s'étagent des plus graves en bas du corps aux plus aigus dans le haut du corps. Je développe ce sujet dans un autre article (Résonances sonores corporelles).
L'oreille est un organe surprenant. Lorsqu'on monte de LA en LA, on a l'impression qu'on ajoute à chaque fois le même intervalle d'une octave. Pour un musicien, l'intervalle d'une octave est égal à 12 demi-tons, soit 6 tons, quelle que soit la hauteur où se situe cette octave. 2 octaves font 12 tons, etc. Or de son côté, le physicien constate la multiplication de la fréquence par 2. En somme l'oreille a la propriété de transformer des multiplications en additions! En mathématique, la fonction qui réalise la même chose s'appelle un logarithme. Cela vous évoque-t-il quelque chose? C'est pourquoi on dit parfois que l'oreille est logarithmique.
Aussi on a inventé une façon de mesurer un intervalle avec une unité qui s'additionne. L'unité la plus simple est l'octave. Un sous-multiple est le demi-ton tempéré défini comme la douzième partie de l'octave. L'unité utilisée par les acousticiens est le centième de demi-ton appelé cent. Il s'ensuit qu'une octave vaut 1200 cents.
Un intervalle entre 2 sons de fréquences f1 et f2 s'exprime par le rapport f1/f2. Le même intervalle exprimé en cents se calcule en passant en logarithmes par la formule: 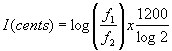 . Les termes 1200 et log2 sont simplement des coefficients d'échelle qui permettent de s'assurer que l'intervalle d'octave, de rapport f1/f2=2,
fait bien 1200 cents.
. Les termes 1200 et log2 sont simplement des coefficients d'échelle qui permettent de s'assurer que l'intervalle d'octave, de rapport f1/f2=2,
fait bien 1200 cents.
Il existe également une unité plus ancienne basée sur les logarithmes. Le physicien Savart a simplement transformé les multiplications de fréquences en additions en appliquant la fonction de logarithme à base 10. Puisque l'octave vaut 2 en rapport de fréquences, la nouvelle mesure d'une octave vaut alors log2 = 0,30103.
Le savart est défini comme le 1/1000 de l'octave, ce qui fait qu'une octave vaut 301 savarts. Tout intervalle entre deux notes de fréquence f1 et f2 vaut 1000 log(f1/f2) savarts.
Le facteur d'échelle (1000) n'est pas tout à fait le même que celui des cents (1200/log2 = 3986), de sorte que 1 savart vaut approximativement 4 centièmes.
Un comma vaut environ 5 savarts.
Quel est le plus petit saut de hauteur que l'oreille peut apprécier?
Écoutez. Entendez-vous le saut de hauteur entre le LA et la fréquence supérieure?
L'oreille perçoit très facilement le demi-ton, mais elle est beaucoup plus performante que ça, bien plus qu'on imagine: il lui est facile de distinguer le 1/10e de ton et même le 1/20e de ton. Une oreille entraînée est capable de discerner le 1/200e de ton dans les fréquences moyennes de sa plage d'audition, soit 1 centième ou une variation de fréquence de 0,05%. Le cent (centième de demi-ton) apparaît comme la plus petite hauteur perceptible.
Sur la figure 5, j'ai reporté les tessitures des voix humaines, des flûtes à bec (flûtes douces), de la guitare et du piano. On remarque que la voix s'étale sur 2 à 3 octaves, tandis que le piano atteint 7 octaves.
Quant à l'oreille, elle peut percevoir environ de 16 à 16 000 Hz soit jusqu'à 10 octaves. En effet, si l'on double la fréquence 10 fois, cela revient à multiplier par 210=1024, très proche de 1000.
Figure 5. Étendues (tessitures) des voix humaines, des flûtes à bec, de la guitare classique et du piano

Gamme, article dans Encyclopaedia Universalis
Je voudrais également citer les logiciels qui m'ont permis de confectionner la plupart des illustrations sonores et visuelles de cet article, Melody Assistant et Audacity, tout simplement parce que je les trouve géniaux et que je voudrais vous faire profiter de ces merveilles. Merci aux créateurs et contributeurs.
Les figures qui montrent des portions de partitions ont été réalisées avec Melody Assistant. "Melody Assistant" est un logiciel dédié à l'écriture et l'impression de musique. Il permet également de restituer la musique écrite et d'enregistrer le fichier sonore correspondant, en format MIDI ou en format audio (MP3, etc.), ce qui a donné une partie de ceux qui sont intégrés dans ce texte. C'est un produit de la société internationale toulousaine Myriad, existant en version française que vous pouvez acquérir pour un prix très modique.
Les enregistrements sonores et créations de sons ont été réalisés avec le logiciel de traitement sonore Audacity en version française. "Audacity" est un véritable petit studio de traitement du son. Il permet d?enregistrer, de jouer, d'importer et d?exporter des données en plusieurs formats dont WAV et MP3. C'est un logiciel libre et gratuit, répondant à la licence GNU.
Je suis pantois devant la puissance actuelle de création des ordinateurs personnels. Nous pouvons transformer notre ordinateur en petit studio musical et atelier d'édition, gratuitement ou presque. Pour réaliser la même chose sur bande magnétique et papier musique il y a 20 ans, j'aurais dû faire appel à un laboratoire d'électronique et à une imprimerie spécialisée, chers, et que bien sûr je n'avais pas à disposition.
Première version 18 octobre 2005
Version révisée et augmentée 5 décembre 2005 (paragraphe "mesure des intervalles")