Gammes et modes musicaux
III- Ton, tempéraments et intonation juste
Science des nombres et sensibilité humaine
Alain Boudet
Dr en Sciences Physiques
Résumé: Pourquoi les interrogations sur la définition du ton et des intervalles constitutifs des gammes ont-elles préoccupé tant de compositeurs et de musicologues depuis l'antiquité grecque? Le ton, la tierce, la quinte, l'octave sont-ils des données absolues? Non, bien au contraire. Au cours du temps, et cela au moins depuis l'antiquité grecque, les intervalles ont été déterminés sur des bases mathématiques et techniques, en faisant appel à la science des nombres, tout en cherchant à s'adapter aux instruments existants. La gamme tempérée a succédé à d'autres gammes, telles que la gamme pythagoricienne, la gamme de Zarlino, et divers systèmes de tempéraments. Elle est une convention passagère, correspondant à la mentalité d'une époque. L'essentiel réside dans l'effet sonore qui résulte de la gamme, et dans la façon dont elle résonne et agit sur le corps et sur l'âme. Des recherches récentes tentent de trouver une intonation qui soit juste pour le corps et pour l'Être. Mais est-ce possible de façon définitive et universelle?
III: Ton, tempéraments et intonation justeContenu de la partie III
Récapitulation des première et deuxième parties: Nous savons qu'un mode est défini par le placement en hauteur, le long de l'échelle d'une octave, d'un nombre limité de notes, généralement 7, mais typiquement entre 5 et 8. Imaginons ces notes comme des échelons dans l'échelle de l'octave. Ces échelons sont appelés les degrés.
Ces 7 (ou autre nombre) degrés peuvent être placés au choix parmi 11 positions possibles sur les montants de l'échelle (positions qu'on peut imaginer comme des encoches sur ces montants). En comptant la position du bas qui est le point de départ, et celle du haut qui est son octave, elles divisent l'octave en 12 demi-tons. Le chiffre 12, fréquent dans la musique de l'Occident, n'est d'ailleurs pas impératif, et dans certaines musiques, l'octave est divisée en parties plus nombreuses et plus petites. Le choix particulier d'un arrangement de positions définit un mode.
Dans cet article, je me penche de façon plus fine sur la façon dont sont déterminés les emplacements des 12 encoches, autrement dit comment sont définis précisément les tons, les demi-tons et en conséquence les autres intervalles. Nous constaterons qu'il y a eu des réponses multiples dans l'histoire de la musique. La façon d'accorder les instruments est le reflet d'une époque, d'un lieu, d'une pensée.
Afin de comprendre cela de façon concrète, je prends pour exemple 3 échelles parmi les plus citées, toutes en mode majeur, mais accordées de 3 façons différentes. Dans notre terminologie contemporaine, elles sont nommées gamme tempérée, gamme de Zarlino ou naturelle, et gamme de Pythagore.
L'intention de cet exposé n'est pas une reconstitution historique. Nous nous questionnons sur la démarche qui conduit à élaborer des gammes déterminées. En découvrant de façon détaillée comment sont définis les intervalles de ces gammes, nous pourrons constater leur variété, et nous pourrons mesurer combien nous sommes conditionnés par des idées reçues sur les gammes et le ton. Cela nous ouvrira de nouvelles perspectives et nous pourrons choisir plus librement, en tant qu'auditeur ou musicien, la musique qui nous fait le plus de bien par ses résonances.
NOTE: Ne vous arrêtez pas sur les tableaux de chiffres si ça ne vous parle pas. Vous pouvez les sauter sans inconvénient. Ils sont seulement là pour décrire les intervalles de façon plus précise afin de montrer la preuve de ce qui est dit.
Pourquoi les modes sont-ils construits avec 7 degrés, ou 5 ou 8 (voir Partie II: défilés de modes)? Et comment la hauteur de ces degrés est-elle fixée de façon exacte? Exemples pratiques: À quelle hauteur un fabriquant d'instruments fixe-t-il les notes de ses instruments? Comment procède un accordeur de piano?
Peut-être vous semble-t-il, d'après les enseignements scolaires et les médias, que les gammes majeures et mineures sont fixées de manière universelle et immuable, selon des lois semblables à la loi de la gravité qui régit l'orbite terrestre ou aux lois physiologiques de la circulation sanguine. Effectivement, les hauteurs des notes des gammes sont déterminées par des principes. Mais ces principes sont-ils basés sur des lois cosmiques ou sont-ils seulement des conventions culturelles, des produits arbitraires de nos esprits?
Les gammes et modes sont les mots d'un langage, et choisir les hauteurs fines des notes ou intonation revient à définir les codes de ce langage. Pourquoi adopter telle grammaire plutôt qu'une autre? Y a-t-il une instance académique internationale qui fixe la définition des notes, comme l'Académie Française définit les mots et leur orthographe?
En réalité, de la même façon que l'humanité nous offre bien des langages très différents, elle nous offre de même des langages musicaux différents, dans lesquels la définition des tons et demi-tons varie beaucoup. Par notre culture occidentale actuelle, essentiellement scolaire, puis "commerciale" et "médiatique" au travers des disques, des diffusions radio et TV, nous sommes conditionnés à écouter de la musique dite "tempérée", dont on verra la définition plus bas. Mais cela n'est le cas ni dans la musique du Moyen Âge, ni dans la musique ethnique, ni dans la pratique réelle du chanteur.
La gamme tempérée semble avoir quelques inconvénients, surtout parce qu'elle ne respecte pas les correspondances harmoniques naturelles avec le corps. Actuellement des chercheurs et des compositeurs développent de nouvelles musiques basées sur les résonances plus naturelles, plus harmoniques, qualité appelée l'intonation juste. Qu'est-ce que ça veut dire, juste?
Je répondrai à cette question plus loin, mais il nous faut d'abord comprendre ce qu'est précisément la gamme tempérée, la gamme habituelle de notre culture de masse. On découvrira qu'elle est d'un usage assez récent, et qu'auparavant on utilisait d'autres systèmes d'intonation, tels que celui de Pythagore et puis d'autres encore. Et que ces systèmes n'étaient pas tempérés ou pas de la même façon.
Pour illustrer notre recherche sur les valeurs fines des intervalles, nous nous restreignons dans cet article au mode majeur, qui imprègne notre culture musicale classique et beaucoup de nos chants populaires.
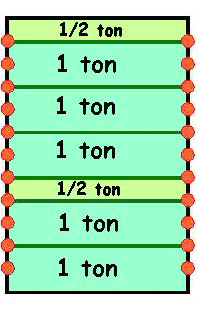
Reprenons le schéma issu de la Partie I qui nous donne la structure du mode majeur. On part du principe que l'échelle totale représente une octave juste. Cela n'est pas toujours vrai, comme on le constatera avec le tempérament Cordier.
Le mode majeur est défini par le choix du placement des 7 échelons sur les 11 encoches de l'échelle (ronds rouges) tel qu'il est représenté sur la figure, donc par le placement des deux demi-tons. Le problème de l'intonation concerne la position fine de ces encoches: où positionner exactement chacun de ces ronds?
À votre avis, comment les emplacements précis des 11 encoches ont-ils été déterminés? Peut-être allez-vous répondre que le schéma en suggère la solution puisque nous y voyons une succession de tons et de demi-tons. Si un ton vaut deux demi-tons, alors il suffit de diviser l'intervalle d'octave en 12 demi-tons identiques, ce qui fixe la position des encoches.
Cette réponse n'est pas exacte en général, mais elle l'est justement en ce qui concerne la gamme à tempérament égal. Ce choix de 12 demi-tons égaux est précisément la définition de la gamme tempérée actuelle (on verra plus bas la signification des termes tempéré et tempérament).
Remarque: Si j'emploie le terme de "gamme" majeure, certains vont penser que je ne suis pas rigoureux puisque selon la définition que j'ai donnée des gammes et des modes dans la première partie, je devrais dire un "mode" majeur. Oui, c'est vrai, mais le langage ne se comporte pas comme un être mathématique rigoureux. En réalité le mot "mode" est déjà contenu dans "majeur", et "gamme majeure" signifie "n'importe quelle gamme en mode majeur". D'ailleurs, dans les pratiques musicales historiques, la distinction entre mode et gamme n'est pas aussi évidente que notre définition rigoureuse des temps modernes, et cela est lié au peu d'importance accordée à la hauteur absolue (voir mon article Sensations sonores: hauteur).
Dans la gamme à tempérament égal (en raccourci "tempérée), les tons sont tous identiques, le demi-ton vaut exactement la moitié d'un ton, l'octave possède 12 demi-tons rigoureusement égaux. Le demi-ton est donc la douzième partie d'une octave juste et les encoches sont disposées à intervalles réguliers d'un demi-ton.
Si l'on veut jouer une gamme chromatique ou changer de tonalité (voir Partie I), c'est très commode parce qu'il suffit de tout décaler d'un certain nombre de demi-tons. Cette gamme est le type auquel la culture médiatique nous a habitués.
Si l'on mesure les intervalles en unités appelées "cents" (voir article Sensations sonores: hauteur), les demi-tons valent 100 cents par définition du cent, les tons valent 200 cents, et l'octave vaut 1200 cents.
Si l'on mesure les intervalles par les fréquences vibratoires des sons, le calcul de leur valeur est un peu plus compliqué. L'octave est caractérisée par le nombre 2 qui est le rapport entre les fréquences de deux notes distantes d'une octave. Par exemple, il y a le même intervalle d'une octave entre le son de fréquence 128 Hz et celui de fréquence 256 Hz, ou entre celui de 20 Hz et celui de 40 Hz. Il s'agit d'un rapport, une multiplication par 2 et non une addition.
Pour partager l'octave en douze intervalles égaux, les mathématiques nous apprennent qu'il ne faut pas diviser 2 par 12, mais utiliser la racine douzième: nous obtenons l'intervalle d'un demi-ton, 12√2, qui s'écrit aussi 21/12, soit 1,0595. C'est le nombre par lequel il faut multiplier (et non ajouter) la fréquence d'une note quelconque pour monter d'un demi-ton: par exemple il y a un intervalle d'un demi-ton entre la note 20 Hz et la note 21,19 Hz ou encore de 128 à 135,616.
En montant une deuxième fois d'un demi-ton, on a le rapport 22/12=1,12246 pour un ton. Et ainsi de suite, jusqu'à retrouver 2 lorsqu'on a multiplié 12 fois.
Dans le tableau I ci-dessous, j'ai reporté les valeurs des intervalles du mode majeur à tempérament égal par rapport à la note de base de la gamme, la tonique (les 3 premières lignes du tableau). Les deux dernières lignes présentent une application particulière de ce schéma dans laquelle la tonique choisie est le DO3, et la fréquence du LA3 est 440 hertz selon la référence internationale, ce qui détermine la valeur des fréquences des autres notes (voir article Sensations sonores: hauteur pour la numérotation des octaves et la détermination d'un diapason international).
Tableau I: Les intervalles de la gamme majeure tempérée par rapport à la note de base
| Intervalles par rapport à la tonique | En cents | 0 | 200 | 400 | 500 | 700 | 900 | 1100 | 1200 |
| En rapport de fréquences (fractionnaire) | 1 | 22/12 | 24/12 | 25/12 | 27/12 | 29/12 | 211/12 | 2 | |
| En rapport de fréquences (décimal) | 1 | 1,1225 | 1,2599 | 1,4167 | 1,4983 | 1,6818 | 1,8877 | 2 | |
| Notes | DO3 | RÉ3 | MI3 | FA3 | SOL3 | LA3 | SI3 | DO4 | |
| Fréquences des notes en hertz repère LA 440 | 261,625 | 293,67 | 329,63 | 349,22 | 391,99 | 440 | 493,88 | 523,25 | |
Le résultat de ces calculs est flagrant: la gamme tempérée est d'une précision mathématique, claire et sans surprise. Les tons et demi-tons s'y échelonnent de façon régulière en 100 ou 200 cents. Si nous sommes de ceux qui n'ont reçu que quelques cours scolaires pour toute éducation musicale, reconnaissons que notre représentation de la gamme est assez conforme à cette vision: un ton doit toujours avoir la même grandeur quoiqu'il arrive et il est défini par les musiciens et les scientifiques! De plus, lorsque nous voyons un piano avec ses touches équidistantes, nous avons une image qui semble confirmer cette représentation.
De même, mon schéma des 11 ronds rouges sur l'échelle ci-dessus peut laisser croire que leur position est bien déterminée à intervalles réguliers, fixée par quelque autorité compétente. Or cette représentation est due à une habitude, une paresse de l'esprit liée au conditionnement ambiant. En réalité, les intervalles ne sont réguliers que dans le cas de la gamme tempérée à laquelle nous sommes habitués, mais elle est loin d'être la seule construction possible. Il existe des variations fines des positions des degrés et des écarts subtils dans la définition des tons et des demi-tons. Ainsi, le demi-ton n'est pas forcément la moitié d'un ton.
Observons que le procédé consistant à définir un ton comme la fraction d'un sixième d'octave dérive plus d'une recherche mentale que d'une sensibilité, même si, comme on le verra plus loin, elle répond à des problèmes pratiques de transposition et de modulation. La gamme tempérée est utilisée seulement depuis la fin du 18e siècle, et généralisée depuis le 19e, après bien des débats et réticences. Elle est le reflet d'une mentalité très moderne de mesure, de normalisation et d'uniformité, qui s'est développée en même temps que la science mécanique et la technique au moment de la "révolution industrielle" du 19e siècle.
Il est souvent dit que c'est J.S. Bach, en composant son œuvre Le clavier bien tempéré, qui a été le promoteur de cette nouvelle gamme, mais cette rumeur est fausse. Car "bien tempéré" n'a pas le sens de tempérament égal, mais de tempérament le meilleur, c'est-à-dire celui qui permet de jouer dans la plupart des 24 tonalités différentes. Les musicologues sont d'avis que Bach s'est opposé à l'usage de la gamme à tempérament égal et qu'il a défendu des systèmes dont le tempérament n'est pas égal (voir plus loin la définition d'un tempérament et ceux probablement employés par J.S. Bach).
Au cours des siècles, beaucoup de recherches ont été conduites sur la définition des intervalles musicaux, par de nombreux musiciens, compositeurs et physiciens, en Occident et aussi en Asie et au Moyen Orient. Même pendant ses heures de gloire, la gamme tempérée a été quelquefois contorsionnée, poussée dans ses retranchements, et ses cadres ont été outrepassés. La musique contemporaine a abandonné la gamme tempérée et s'est dirigée vers d'autres formes (voir article Évolution de l'expression musicale occidentale). Et oui, car le monde est vaste, créatif et diversifié (voir partie II, Défilé de modes). Le tempérament égal n'est pas utilisé dans les musiques extra-européennes, ni, à l'origine, dans les musiques traditionnelles.
En conséquence la gamme tempérée n'est pas un modèle absolu. Elle ne constitue qu'une convention passagère, et ce mot "convention" n'est pas péjoratif. Car elle est à l'origine d'un foisonnement créatif et source d'œuvres magnifiques. Cela témoigne simplement d'une évolution constante de la musique, à l'image de l'être humain et de la vie, évolution parsemée de moments de repos et d'intégration pendant lesquels on profite des nouveaux acquis.
Mais alors, quelles étaient les gammes employées en Europe avant le 19e siècle? La musique de la Renaissance (16e siècle) s'est beaucoup fondée sur les recherches de Zarlino et sur des systèmes de tempéraments inégaux, en particulier le système mésotonique. Ils ont eux-mêmes remplacé le système dit "pythagoricien" employé au Moyen-Âge.
À titre d'exemple très instructif, étudions la gamme majeure bâtie sur le système de Zarlino. Elle va nous conduire à la notion d'intervalle juste et naturel.
De tout temps, les compositeurs et philosophes érudits se sont interrogés sur les valeurs à attribuer aux intervalles et sur la construction des modes. De nombreux écrits nous sont parvenus, relatant les recherches de quelques-uns d'entre eux depuis l'antiquité grecque jusqu'à nos jours (voir La hauteur des notes de musique doit-elle être normalisée par un diapason?).
Portrait de Gioseffo Zarlino, 1599
Merci à Musée international et bibliothèque de la Musique de Bologne
Gioseffo Zarlino (1517-1590) est l'un d'entre eux. Compositeur italien de la Renaissance, il a mené des études approfondies sur les modes de l'antiquité grecque, issus des enseignements de Pythagore. Il leur reprochait d'avoir des tierces dissonantes et a été amené à proposer un ajustement des intervalles qui assure la justesse des tierces principales. La notion de gamme de 7 notes n'existait pas alors, et il travaillait sur des tétracordes ou hexacordes (4 ou 6 notes successives) - (voir l'article La hauteur des notes de musique doit-elle être normalisée par un diapason?).
Zarlino se réfère aux travaux de l'astronome grec Claude Ptolémée (vers 90 - 168) exposés dans son traité de musicologie Harmoniká, dans lequel il défend des intervalles musicaux basés sur des proportions mathématiques.
On ne sait pas si le système de Zarlino a été appliqué en pratique car il est resté surtout théorique, mais il a alimenté réflexions et expérimentations à ce sujet. Au 16e siècle, on employait surtout le tempérament mésotonique (voir plus bas sur les tempéraments).
Oublié par la suite, le système de Zarlino a retrouvé de l'intérêt au 19e siècle avec le physicien allemand Hermann von Helmholtz (1821 - 1894). Celui-ci étudie les lois acoustiques et propose une gamme naturelle basée sur des intervalles issus des résonances physiques naturelles, afin de respecter une certaine perfection harmonique dans la justesse des intervalles. C'est le système de Zarlino renouvelé dans une gamme de 7 notes, et conforté par les lois physiques des harmoniques, d'où son nom de gamme de Zarlino, qu'il serait plus juste de nommer gamme de Helmholtz.
Lorsqu'une note tenue est émise, le son contient un son fondamental accompagné de résonances physiques naturelles appelées sons harmoniques de cette note. Physiquement, les sons harmoniques sont caractérisés par la valeur typique de leur fréquence: elle est un multiple de la fréquence du son de base (pour la nature et la définition des harmoniques, voir article Sensations sonores: le timbre). Du moins en théorie, car en pratique on a mis en évidence un léger phénomène d'inharmonicité (écart par rapport à la valeur multiple dans le cas des cordes tendues - voir plus bas).
Voici, dans le tableau II ci-dessous, les harmoniques d'un son de base, DO1, fixé soit à 64 Hz, soit à 66 Hz. Le nombre de la première ligne indique le numéro d'ordre de l'harmonique, mais il est également le facteur par lequel il faut multiplier la fréquence de base pour obtenir la fréquence de l'harmonique.
Les sons harmoniques, que l'oreille entend clairement superposés à la note de base, ont depuis longtemps attiré l'attention dans la pratique vocale, instrumentale et spirituelle. Ils sont exploités dans le chant harmonique ou diphonique. Ils sont à la base de l'accordage d'instruments comme le violon ou le piano.
Les intervalles naturels sont ceux qui naissent entre les sons harmoniques. La gamme de Zarlino est construite sur la base de ces intervalles. Examinons-les.
Revenons au tableau II. La valeur 66 hertz pour la fréquence du DO1 est choisie à titre d'exemple, un nombre rond très proche de la fréquence 65,4 qui est celle du DO1 dans la gamme tempérée examinée plus haut (251,63/4). La fréquence de l'harmonique 12 est 12 fois plus grande, soit 792 Hz. C'est un SOL4 (4e ligne).
Un autre exemple est celui du DO1 fixé à 64 Hz (3e ligne), qui a eu la faveur de physiciens dès le 18e siècle (par exemple Joseph Sauveur) et du compositeur Giuseppe Verdi au 19e siècle, sous prétexte qu'il est une puissance de 2 (2x2x2x2x2x2) et qu'il apparait donc comme plus scientifique (voir l'article La hauteur des notes de musique doit-elle être normalisée par un diapason?).
Tableau II: Harmoniques naturelles de DO1. Le nombre de la première ligne indique le numéro d'ordre de l'harmonique, mais il est également le facteur qui donne la fréquence de l'harmonique, en le multipliant par la fréquence de base.
On peut repérer l'accord parfait majeur (bleu sombre), l'accord parfait mineur (marron) et les 5 notes de la gamme pentatonique (en gras dans l'octave 4).
| Rapport des fréquences | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Valeur de la fréquence (base DO1=66) | 66 | 132 | 198 | 264 | 330 | 396 | 462 | 528 | 594 | 660 | 726 | 792 | 858 | 924 | 990 | 1056 | 1122 | 1188 |
| Valeur de la fréquence (base DO1=64) | 64 | 128 | 192 | 256 | 320 | 384 | 448 | 512 | 576 | 640 | 704 | 768 | 832 | 896 | 960 | 1024 | 1088 | 1152 |
| Nom de la note | DO1 | DO2 | SOL2 | DO3 | MI3 | SOL3 | (sib) | DO4 | RÉ4 | MI4 | (fa#) | SOL4 | (sol#) | (sib) | SI4 | DO5 | (do#) | RÉ5 |
La suite de ces fréquences inclut des notes constitutives de la gamme majeure, et d'autres qui ne le sont pas. Pour ces dernières, la note la plus proche est indiquée entre parenthèses.
Dans le tableau II, j'ai exprimé les intervalles en fréquences et non en cents qui sont pourtant plus parlant dans une gamme! Et bien, je le ferai plus loin.
Toutefois, ce qui vient en premier dans l'étude des intervalles sont les rapports de fréquence, comme il apparaît dans le tableau II des harmoniques. Historiquement, le rapport entre les notes était le seul moyen physique de mesurer les intervalles. Comment les anciens pouvaient-ils mesurer des fréquences sans appareil électronique?
Tout comme ses prédécesseurs grecs, médiévaux et ses contemporains, Zarlino se servait d'instruments à cordes, les monocordes, conçus dans ce but. Ils étaient faits d'une corde tendue entre les deux extrémités d'une planchette (voir figure ci-contre). Un chevalet mobile, sorte d'arête, partageait la corde en deux. La hauteur des notes émises par chacune des portions de corde de part et d'autre du chevalet est en relation directe avec leur longueur.
Aussi, on mesurait un intervalle entre deux notes par le rapport, non pas des fréquences, mais des longueurs de corde correspondantes. Or, il a été montré plus tard par des physiciens tels que Helmholtz que le rapport des fréquences est exactement l'inverse des rapports de longueur. Autrement dit, si vous divisez la longueur de la corde par 2, sa fréquence sonore est multipliée par 2 et vous obtenez l'octave! Dans ses ouvrages, Zarlino rapporte la longueur des cordes et les compare en faisant leur rapport. 1/2 pour l'octave, 2/3 pour la quinte, etc.
Plus de détails sur l'historique de la mesure des intervalles et des fréquences dans l'article La hauteur des notes de musique doit-elle être normalisée par un diapason?
IMAGE: Un monocorde, d'après les écrits de Zarlino
Dans le tableau II des harmoniques, on remarque la succession de 5 notes de la gamme de l'octave 4: DO, RÉ, MI, SOL, SI.
Remarque de navigation: ne craignez pas de vous rendre à ce tableau en cliquant sur le lien, car vous avez la possibilité de revenir ensuite ici-même pour la suite de votre lecture en utilisant, dans la barre de menu de votre navigateur, la flèche gauche "Revenir à la page précédente", ou alternativement sur le clavier: ALT+flèche gauche pour Windows, CMD+flèche gauche pour Mac.
On ramène ces notes de l'octave 4 à l'octave 3, afin de les comparer avec cette même octave de la gamme tempérée (tableau I). Pour cela, on divise les fréquences par 2 (pour obtenir RÉ3 et SI3). Le résultat est rapporté dans le tableau III.
Tableau III: Les intervalles de la gamme majeure de Zarlino, par rapport à la note de base
| Intervalles par rapport à la tonique | En cents | 0 | 204 | 386 | 498 | 702 | 884 | 1088 | 1200 |
| En rapport de fréquences (fractionnaire) | 1 | 9/8 | 5/4 | 4/3 | 3/2 | 5/3 | 15/8 | 2 | |
| Notes | DO3 | RÉ3 | MI3 | FA3 | SOL3 | LA3 | SI3 | DO4 | |
| Fréquences des notes en hertz repère LA 440 | 264 | 297 | 330 | 352 | 396 | 440 | 495 | 528 | |
| Fréquences des notes en hertz repère DO 256 | 256 | 288 | 320 | 341,3 | 384 | 426,6 | 480 | 512 | |
Note de lecture: Les paragraphes écrits en retrait et en petits caractères comme celui-ci sont des développements techniques que vous pouvez sauter sans inconvénients, pour une lecture plus fluide.
Calcul des intervalles: Pour calculer l'intervalle entre une note donnée et la note de base DO3, on fait le rapport entre sa fréquence et celle du DO3 (voir le tableau III). Par exemple, le rapport entre le MI 3 (harmonique 5) et le DO 3 (harmonique 4) est 5/4.
Remarquons qu'à ce stade, nous avons obtenu seulement 5 notes. Les deux notes manquantes FA et LA ne sont pas des harmoniques du DO. On obtient donc une gamme à 5 notes, dite pentatonique.
DO - RÉ - MI - SOL - SI - (DO)
Puisque les intervalles sont définis par des harmoniques, c'est-à-dire des nombres entiers par rapport au son fondamental, leurs valeurs sont des fractions
de nombres simples:
quinte: 3/2 (SOL, harmonique 3 de DO)
tierce majeure: 5/4 (MI, harmonique 5 de DO)
Le nom de quinte provient de la position de la note correspondante (SOL) au cinquième degré de la gamme. Le nom de tierce indique le troisième degré.
De plus, on remarque que les rapports des intervalles entre harmoniques proches sont des fractions dont le numérateur est plus grand d'une unité que le dénominateur: (2+1)/2 pour la quinte; (4+1)/4 pour la tierce. C'est ce que les anciens appelaient un rapport épimore ou superparticulaire. Cette simplicité des nombres est devenue un principe dans la recherche des autres intervalles; en langage moderne, on pourrait dire une sorte d'esthétique.
Si à la tierce majeure et la quinte juste, nous ajoutons la tonique, alors nous obtenons l'accord parfait majeur. Il est parfaitement apparent dans la succession des harmoniques du tableau II, à l'octave 4 où se succèdent DO4, MI4 et SOL4.
Un autre accord parfait majeur est naturellement présent dans cette gamme de 5 notes, celui de SOL (SOL - SI - RÉ), avec les mêmes intervalles naturels.
Vérifions que cet accord a bien la structure d'un accord parfait majeur:
SOL 4, son fondamental, harmonique 12
SI 4, harmonique 15, soit un intervalle 15/12=5/4, qui est bien la tierce majeure.
RÉ 5, harmonique 18, soit un intervalle 18/12=3/2, qui est bien la quinte juste.
Les harmoniques 10, 12 et 15 donnent l'accord parfait mineur: MI, SOL, SI.
Si l'on veut disposer d'une gamme majeure à 7 notes, dite heptatonique, on doit ajouter à ces 5 notes naturelles une quarte (FA) et une sixte (LA).
Remarquons que la quinte SOL sépare l'octave en deux parties: de DO à SOL (une quinte, intervalle de 5 notes consécutives) et de SOL à DO (une quarte, intervalle de 4 notes consécutives). C'est donc là qu'apparait l'intervalle de quarte.
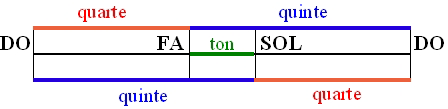
La symétrie de la quinte et de la quarte entre les deux extrémités de l'octave
On trouve le FA en reportant l'intervalle de quinte en descendant à partir du DO supérieur.
Calcul de l'intervalle DO - FA:
Le DO supérieur a pour valeur 2. Reportons un intervalle de quinte (3/2) en descendant. Nous arrivons à FA dont la hauteur par rapport au DO inférieur est: 2/(3/2)=4/3
La quarte est définie par sa valeur de 4/3 qui, remarquons-le, est également un intervalle épimore: (3+1)/3. On a le même intervalle de quarte 4/3 entre DO3 - FA et entre SOL - DO4.
Observons cette symétrie quarte +ton +quarte, présente également dans la gamme tempérée.
Pour obtenir le LA (sixte de DO), on construit un troisième accord parfait majeur sur la base du FA (FA, LA, DO).
Calcul de l'intervalle DO - LA:
FA, son fondamental: 4/3
LA, tierce de FA: (4/3)x(5/4)=5/3
DO, quinte de FA: (4/3)x(3/2)=2
Après la quinte (3/2), la tierce (5/4) et la quarte (4/3), on trouve que la sixte est définie par le rapport 5/3 (tableau III).
Nous disposons à présent de toutes les notes de la gamme majeure naturelle de Helmholtz/Zarlino. Il résulte de cette recherche que la gamme de Zarlino est entièrement générée par les harmoniques 3 et 5. Le 3 engendre la quinte, puis la quarte par renversement de la quinte, et le 5 engendre la tierce et la sixte.
Alors nous pouvons nous poser la question: en quoi cette gamme diffère-t-elle de la gamme tempérée?
Pour faciliter la comparaison de ces nouveaux intervalles, il est judicieux de convertir les valeurs fractionnaires en cents (voir le tableau III). On constate immédiatement des différences dans la définition du ton: de valeur 200 cents dans la gamme tempérée, il passe à 204 cents dans la gamme de Zarlino. Quant à la quinte SOL, elle est de 702 cents au lieu des 700 cents de la gamme tempérée. La tierce majeure est beaucoup plus petite, 386 cents au lieu de 400.
Cela a-t-il une incidence sur la justesse de l'intonation vocale et instrumentale? Je reporte cette discussion un peu plus loin, afin de lui inclure la gamme dite de Pythagore qu'il est temps de présenter ci-dessous.
Les compositeurs, du Moyen-Âge au 16e siècle, utilisaient les modes liturgiques reposant sur un système d'intervalles dérivé des études de Pythagore (sur les modes liturgiques, voir Partie II, Défilé de modes).
Pythagore a vécu en Grèce au 6e siècle avant Jésus-Christ (vers 580 av.J.C. - vers 495 av.J.C.). Les collégiens connaissent bien le théorème de Pythagore sur les triangles rectangles, mais ce qu'ils ignorent, ainsi que la plupart de leurs professeurs, c'est qui était réellement Pythagore, et pourquoi il s'est impliqué dans l'étude des triangles et dans celle des gammes. Or il mérite d'être plus amplement connu, aussi vais-je donner quelques informations à son sujet.
Pythagore, sage et initié, a fondé une école des mystères qui accueillait de nombreux disciples à Crotone dans le Sud de l'Italie, qui faisait alors partie de la Grande Grèce. Auparavant il avait voyagé et passé 22 ans de sa vie en Égypte où il avait été accueilli par le pharaon Amosis et initié aux connaissances égyptiennes par les prêtres. Au moment de l'invasion de l'Égypte par les Perses, il fut fait prisonnier et emmené à Babylone où il passa une douzaine d'années au contact de la philosophie de Zoroastre. De ces formations, il a retiré sa propre doctrine et ses connaissances sur l'être humain, l'âme, le cosmos, la géométrie, les nombres.
À ses disciples, Pythagore enseignait que le nombre n'est pas une quantité abstraite comme le considéraient les profanes, mais un principe vivant et sacré, issu de l'harmonie cosmique. Les nombres représentent les forces divines en action dans le monde, dans l'être humain et dans la musique. La tradition rapporte que le cosmos est engendré par quatre nombres essentiels: de 1 à 4. En les additionnant ou les multipliant, on retrouve tous les autres. D'autres chiffres ont une grand importance: le 7, le 10 et le 12.
Le 1 est le nombre de l'origine, l'Unité primordiale, l'Essence de Dieu, la Monade. Le monde, malgré sa diversité, n'est qu'une unité. Toute action d'un individu réagit sur l'Univers entier, de même qu'un individu subit les influences de l'Univers entier. L'Être humain n'est pas séparé de l'Univers, de même que la goutte d'eau est une partie de l'océan. L'être humain se présente selon différentes facettes, certaines qu'il aime et d'autres qu'il déteste, mais s'il veut évoluer, il doit s'élever dans une vision globale et réunir ses facettes bonnes et mauvaises en une seule unité (voir aussi l'article L'enfant intérieur et le langage des émotions).
Le 2 exprime la dualité qui consiste à se dédoubler pour se voir, se contempler. C'est la Dyade qui représente nos polarités, en premier la polarité masculin/féminin, qui est la faculté créatrice et régénératrice (voir article Masculin et féminin). En eux-mêmes, les chiffres pairs portent une tonalité féminine. Se dédoubler, c'est prendre de la distance par rapport à soi, mais on reste soi. Le 2 engendre l'octave, qui n'est que la même note répétée à un autre niveau. Pour en sortir, le 2 doit être fécondé par le 3, premier nombre impair, de tonalité masculine.
Le 3 exprime la manifestation, la création, le monde réel. C'est la Triade ou Trinité, le père, la mère et le fils, que l'on trouve non seulement dans la doctrine chrétienne (le Saint-Esprit est l'aspect féminin, la sève de Dieu qui coule dans le corps, bien que cela n'ait pas été conservé comme tel par l'église), mais également dans les théogonies indienne, chinoise, égyptienne, babylonienne, celte. C'est la constitution ternaire de l'être humain, corps physique, âme et esprit. Le 3 engendre la quinte. C'est la première note qui se distingue de la note de base, et qui, comme on va le voir, engendre à elle seule les 7 degrés de la gamme et les 12 notes chromatiques.
Le 7 est un développement de la manifestation qui exprime la loi de l'évolution, la réalisation complète, l'union du 3 et du 4, de l'homme et de son aspect divin. Le 7 a été projeté dans les 7 jours de la semaine, les 7 couleurs de l'arc-en-ciel qui sont en fait la représentation symbolique des 7 rayons créateurs de l'univers (voir article La couleur), les 7 notes de la gamme et le 7 modes de Pythagore (voir Partie II, Défilés de modes).
Le 10 représente la Décade sacrée, les dix doigts de la main, la perfection.
Un aspect plus évolué de l'univers et de l'être humain repose sur la structure du 12. On le trouve dans les 12 mois de l'année, les 12 constellations zodiacales, et les 12 degrés chromatiques. La somme 3+7+12=22 est également un nombre sacré, représenté dans les 22 lames du tarot, elles-mêmes traduisant les couches que l'être humain doit traverser et intégrer pour devenir un initié.
Ces nombres apparaissent également dans le nombre de chakras actifs dans l'être humain, traditionnellement 7, mais qui deviennent progressivement 8, puis 12, puis 22 au fur et à mesure du développement spirituel du disciple (voir article Les corps subtils et les chakras).
À l'époque de Pythagore et au Moyen-Âge, on ne parlait pas de gamme, notion qui était inconnue, mais de tétracordes et d'hexacordes (voir article La hauteur des notes de musique doit-elle être normalisée par un diapason?). On ne sait pas jusqu'à quel point Pythagore a lui-même poussé son étude des intervalles. Beaucoup parmi ses disciples se sont emparé du problème et ont cherché à condenser les lois cosmiques des nombres dans la gamme, même plusieurs siècles après. De nombreux écrits rapportent leurs tentatives et leurs résultats: ceux de Platon, de Boèce, d'Euclide. Or dans ces écrits, plusieurs systèmes s'affrontent.
Le pythagoricien Archytas retient les intervalles de la forme 2/1 (octave), 3/2 (quinte), 4/3 (quarte) que nous avons rencontrés plus haut dans cet article. Il les étend à tous les intervalles de rapports épimores (n+1)/n, autrement dit du rapport de 2 chiffres qui se suivent: 5/4 (tierce majeure), 6/5 et 7/6 (tierces mineures). On va aussi trouver des tons de plusieurs grandeurs: 9/8, 10/9 et 16/15, plusieurs demi-tons tels que 16/15 et 25/24 et enfin des intervalles plus petits ou micro-intervalles.
Le quart de ton (attention, ce n'est pas le quart d'un ton!) était utilisé dans certaines échelles de la musique grecque antique. Il était appelé diesis. Son étendue varie selon les théoriciens: 36/35, 28/27, 39/38, 40/39, 31/30, 32/31. Zarlino a appuyé sa théorie sur ce système.
Un autre disciple, Philolaos, s'appuyait sur les quintes. Il semble que c'est ce système, explicité 6 siècles après la période de Pythagore par Nicomaque de Gérase, qui constitue ce qu'on appelle dorénavant le système diatonique pythagoricien.
Les deux théories des pythagoriciens (épimores et quintes) ont diffusé à partir de la Grèce, et ont été reprises, étudiées, transformées, complétées en Turquie, Perse, Asie centrale. Elles sont une des sources des musiques qu'on appelle maintenant arabes. Par exemple, le grand musicien persan Ziryab (789 - 857) les aurait connues. En quittant Bagdad pour s'installer en Andalousie, il est à l'origine de la musique arabo-andalouse, la Nouba (voir Partie II, défilés de modes).
La gamme élaborée au Moyen-Âge d'après Pythagore est bâtie comme celle de Zarlino sur les résonances physiques naturelles, les harmoniques. Mais elle ne retient que les deux premières harmoniques, 2 (octave) et 3 (quinte), et non l'harmonique 5 (tierce) comme Zarlino le fera plus tard. Les deux nombres 2 et 3 ont une importance fondamentale, ainsi que leurs combinaisons qui vont générer tous les intervalles. En premier lieu l'intervalle 3/2 qui est la quinte.
Notons en passant combien ces gammes qualifiées de naturelles reposent sur des études réfléchies et élaborées.
Si l'on part de DO3 en position 0, on monte de quinte en quinte en multipliant par 3/2, et on descend en divisant par 3/2, c'est-à-dire en multipliant par 2/3, ce qui donne:
Tableau IV: Suite des quintes à partir de DO
| Numéro d'ordre | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|---|---|
| Rapport | (2/3)2=4/9 | 2/3 | 1 | 3/2 | (3/2)2=9/4 | (3/2)3=27/8 | (3/2)4=81/16 | (3/2)5=243/32 | (3/2)6=729/64 |
| Note | SIb1 | FA2 | DO3 | SOL3 | RÉ4 | LA4 | MI5 | SI5 | FA#6 |
On obtient la gamme majeure pythagoricienne en rassemblant les 7 notes de -1 à 5 dans la même octave (tableau V).
Tableau V: Les intervalles de la gamme majeure pythagoricienne par rapport à la note de base
| Intervalles par rapport à la tonique | En cents | 0 | 204 | 408 | 498 | 702 | 906 | 1110 | 1200 |
| En rapport de fréquences (fractionnaire) | 1 | 9/8 | 81/64 | 4/3 | 3/2 | 27/16 | 243/128 | 2 | |
| Notes | DO3 | RÉ3 | MI3 | FA3 | SOL3 | LA3 | SI3 | DO4 | |
| Fréquences des notes en hertz repère LA 440 | 260,74 | 293,33 | 330 | 347,65 | 391,11 | 440 | 495 | 521,48 | |
Calcul des notes de la gamme: FA3 vient de FA2 en multipliant par 2, ce qui élève d'une octave: de 2/3 à 4/3. RÉ3 vient de RÉ4 en divisant par 2, ce qui abaisse d'une octave: de 9/4 à 9/8. MI3 vient de MI5 en divisant par 4, soit de 81/16 à 81/64. SI3 vient de SI5 en divisant par 4, soit 243/128.
Nous sommes maintenant en mesure de comparer ces gammes, d'évaluer leurs différences, leur importance et leur intérêt, en rassemblant les tableaux I, III et V en un seul tableau récapitulatif synthétique, complété (tableau VI).
Les chiffres et vous: Ne vous laissez pas effrayer par la complexité du tableau et l'abondance de chiffres, car ceux-ci ne sont pas indispensables pour en comprendre les conclusions. Je les rapporte pour ne pas en priver ceux qui ont cette culture des chiffres et qui peuvent les utiliser dans leurs propres recherches et applications.
Quant à ceux qui veulent comprendre la démarche sans entrer dans le détail des chiffres, je les guiderai à travers ce tableau en prenant seulement quelques exemples caractéristiques, au fur et à mesure de l'article. Voici pour commencer une présentation du tableau:
Explications pour lire le tableau: Il est divisé en trois sections correspondant à chacune des gammes (tempérée, Helmholtz/Zarlino, Pythagore). Sur les premières lignes de chacune des sections, on retrouve les données des tableaux I, III, et V dans un ordre un peu différent:
Note mathématique. Comment passer d'une valeur fractionnaire à une valeur en cents: Si les fréquences de 2 sons sont f1 et f2, leur intervalle a pour mesure le rapport f1/f2, exprimé soit en valeur fractionnaire, soit en valeur décimale, en effectuant le calcul de la fraction. Le même intervalle peut être exprimé en cents (une octave = 1200 cents). Pour cela, il faut utiliser la fonction logarithme qui permet de transformer des rapports qu'on multiplie et divise, en intervalles qu'on ajoute ou retranche. L'intervalle entre f1 et f2 se calcule par la formule: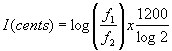 
, où 1200 et log2 sont des coefficients d'échelle qui permettent de garantir que l'intervalle d'octave, de rapport f1/f2=2, fait bien 1200 cents (voir article Sensation sonore: hauteur)
Tableau VI: Tableau récapitulatif des 3 gammes majeures et de leurs intervalles
Au lieu de considérer l'intervalle d'une note par rapport au DO de base, donc entre DO et RÉ, puis DO-MI, DO-FA, il est instructif de comparer les intervalles de ces trois gammes entre notes successives DO-RÉ, RÉ-MI, MI-FA etc. On les trouve dans les lignes inférieures du tableau pour chacune des gammes:
Bien que dans toutes les gammes, les notes consécutives sont séparées par des tons et des demi-tons selon un schéma fixe qui est la définition même de la gamme majeure, on peut constater que les tons et les demi-tons ont des valeurs différentes selon les gammes.
Dans une gamme tempérée, les demi-tons sont obtenus par la division de l'octave en 12 parties égales. Un demi-ton vaut 100 cents et un ton vaut 2 demi-tons, soit 200 cents. C'est mathématique et inexorable.
Dans la gamme pythagoricienne, la ligne 30 du tableau montre clairement les deux sortes d'intervalles, le ton de 204 cents (ou 9/8), dit ton diatonique, et le demi-ton de 90 cents (256/243). Toutefois, on note que contrairement à la gamme tempérée, le demi-ton est plus petit que la moitié du ton. Il ne faut pas se laisser influencer par la terminologie.
Remarque de navigation: ne craignez pas de vous rendre au tableau VI en cliquant sur le lien proposé chaque fois que vous avez envie, car vous avez la possibilité de revenir ensuite ici-même en utilisant, dans la barre de menu de votre navigateur, la flèche gauche "Revenir à la page précédente" ou l'équivalent par les touches du clavier.
Dans la gamme de Zarlino, ça se complique. La ligne 20 du tableau fait apparaitre, non plus deux mais trois types d'intervalles.
Il y a une valeur pour le demi-ton: 112 cents ou 16/15, nettement plus grand que celui de la gamme pythagoricienne (90 cents) et que celui de la gamme tempérée (100 cents).
Le ton peut prendre deux valeurs:
La différence entre les deux tons est (10/9)/(9/8)=80/81 ou 21,5 cents. Elle est nommée un comma syntonique (ne pas confondre avec le comma pythagoricien entre DO# et RÉb examiné plus bas).
Au-delà des chiffres, les différences de tons et demi-tons d'une gamme à l'autre semblent minimes. Sont-elles perceptibles à l'oreille? Oui, plus ou moins selon la sensibilité de l'auditeur et son entrainement. S'il est difficile de percevoir un intervalle de 4 cents, 10 cents sont déjà tout à fait audibles (voir article Sensation sonore: hauteur).
Les différences de tons et demi-tons se répercutent dans les autres intervalles, en particulier dans la quinte, la quarte et la tierce qui jouent des rôles majeurs dans le rendu sonore des mélodies.
Rappelons qu'il existe une symétrie de la quarte et de la quinte insérées dans l'octave. Un ton central (FA-SOL) y est encadré de deux quartes.
Dans la gamme tempérée, le ton de 200 cents est encadré de deux quartes de 500 cents, soit le schéma:
500 (quarte) - 200 (ton) - 500 (quarte) = 1200
Cela donne une quinte de 700 cents.
Dans les systèmes de Zarlino et Pythagore, on a exactement le même schéma:
498 + 204 + 498 = 1200
La quinte vaut 702 cents.
La tierce majeure DO-MI de deux tons vaut 400 cents
La tierce mineure est l'intervalle MI-SOL, un ton + un demi, qui vaut: 300 cents
Tierce majeure DO-MI: 408 ou 81/64
Tierce mineure MI-SOL: 294 ou 32/27
Tierce majeure DO-MI: 386 ou 5/4
Elle est nettement plus petite que les précédentes, -14 cents par rapport à la gamme tempérée et -22
cents par rapport à la gamme pythagoricienne. C'est l'une des différences les plus importantes avec la gamme de Pythagore et la raison essentielle des modifications de Zarlino.
Tierce mineure MI-SOL: 316 ou 6/5. A l'inverse, elle est plus grande de +16 cents par rapport à la gamme tempérée et + 22 cents par rapport à la gamme pythagoricienne.
Pour apprécier la différence entre les tierces, le mieux est d'écouter: successivement la tierce majeure de Zarlino dite juste (386 cents), la tierce majeure tempérée (400), plus grande, et la tierce pythagoricienne (408).
Qu'avez-vous perçu? Vous me direz peut-être qu'il n'y a pas là de quoi en faire tout un article.
Cependant, pour estimer cette différence à sa juste importance, il faut tenir compte de deux phénomènes. Le premier est que la sensibilité de l'oreille a été émoussée par l'habitude d'écouter de la musique tempérée, et peut-être encore plus par une protection contre le monde bruyant dans lequel nous vivons.
Le deuxième est que ces différences sont amplifiées par des battements (variations régulières du volume sonore) qui surviennent lorsqu'on produit ensemble des notes qui ne sont pas dans un rapport harmonique. Sous ce point de vue, et selon l'opinion de certains, la gamme tempérée est fausse. Aussi, nous sommes à nouveau dans une période de recherche de l'intonation juste, c'est-à-dire qui respecte le plus possible les intervalles naturels basés sur les harmoniques.
Dans la pratique vocale et instrumentale, ces différences ont des implications que je vais tenter d'examiner. Toutefois, dans le souci d'être complet et d'expliquer certaines notions sur les demi-tons, je fais un passage par la gamme chromatique.
Nous avons défini les 7 notes de la gamme majeure. Il reste à définir les 5 autres notes sur les 12 que comporte l'échelle chromatique. Les mélodies ne restent pas figées sur les 7 notes de base et passent par des modulations où elles s'aventurent dans les chromatismes. Ces autres notes sont DO#, RÉ#, FA#, SOL# et LA# ou leurs équivalents avec les bémols.
Pour cela, il suffit d'étendre le procédé employé pour définir les 7 notes de base, ce qui va donner des réponses différentes pour chacune des gammes.
Dans le cas de la gamme tempérée, rien de plus simple. Un demi-ton est strictement un demi-ton de 100 cents. De cette manière, on place les notes intermédiaires bien au centre du ton. Le DO# et le RÉb sont identiques et placés à mi-chemin entre le DO et le RÉ (tableau VII).
La logique du cycle des quintes qui est à la base de la gamme de Pythagore fournit également les notes chromatiques.
En continuant à monter de quinte en quinte au-delà du SI5, on génère FA#, DO#, SOL#, RÉ#, LA#.
Le premier dièse apparait avec la 6e quinte construite à partir du DO3. C'est le FA# (voir plus haut le tableau des quintes). Le FA# sépare le ton FA-SOL en 2 demi-tons inégaux, FA-FA# et FA#-SOL. Les résultats qui suivent sont synthétisés sur le tableau VII.
Calcul du FA#: Le FA#6 a pour valeur 36/26=729/64 (tableau IV). En le ramenant à l'octave 3, on génère le FA#3: 36/29=729/512.
Calcul de l'intervalle FA-FA#: C'est le rapport des valeurs de FA# (36/29) et de FA (22/3), soit: FA-FA#: 37/211 ou (729/512)/(4/3) = 2187/2048 = 1,0679 ou encore 114 cents.
L'intervalle FA-FA# est le plus grand. Il vaut 114 cents. C'est le demi-ton chromatique. Situé entre 2 notes de même nom (FA et FA#), il est appelé chromatique comme si le dièse ajoute une couleur à la note.
La valeur de FA#-SOL est plus petite et vaut 90 cents. C'est le demi-ton diatonique, qui se trouve déjà dans la même gamme entre MI et FA, ou SI et DO. Dans le mot diatonique il y a dia- qui signifie 2, donc "distinct", car il est situé entre deux notes de noms différents (FA# et SOL). Toutefois, l'origine du mot remonte à la distinction entre le système de Pythagore appelé diatonique et celui de Zarlino appelé syntonique.
Ainsi le ton pythagoricien de 204 cents est la somme d'un demi-ton chromatique de 114 cents et d'un demi-ton diatonique de 90 cents.
Tableau VII: Gamme chromatique, valeur des demi-tons
| Gamme tempérée | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Notes | DO | réb=DO# | Ré | Mib=RÉ# | MI | Fa | Solb=Fa# | Sol | ||||
| Intervalle par rapport à la tonique | En rapport de fréquences (décimal) | 1 | 1,0595 | 1,12246 | 1,18921 | 1,25992 | 1,3348 | 1,41421 | 1,49830 | |||
| En cents | 0 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | ||||
| Intervalles par rapport à la note précédente | En rapport de fréquences (décimal) | 1 | 1,0595 | 1,0595 | 1,0595 | 1,0595 | 1,0595 | 1,0595 | 1,0595 | |||
| En cents | 0 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | ||||
| Gamme d'après Pythagore | ||||||||||||
| Notes | DO | réb | DO# | Ré | Mib | Ré# | MI | Fa | Solb | Fa# | Sol | |
| Intervalle par rapport à la tonique | En rapport de fréquences (fractionnaire) | 1 | 28/35 256/243 | 37/211 2187/2048 | 32/23 9/8 | 25/33 32/27 | 39/214 19683/16384 | 34/26 81/64 | 22/3 4/3 | 210/36 1024/729 | 36/29 729/512 | 3/2 |
| En cents | 0 | 90 | 114 | 204 | 294 | 318 | 408 | 498 | 588 | 612 | 702 | |
| Par rapport à la note précédente | En rapport de fréquences (fractionnaire) | 1 | 37/211 | 28/35 | 37/211 | 28/35 | 28/35 | 37/211 | 28/35 | |||
| 28/35 | 37/211 | 28/35 | 37/211 | 28/35 | 37/211 | |||||||
| En cents | 0 | 90 | 24 | 90 | 90 | 24 | 90 | 90 | 90 | 24 | 90 | |
De façon symétrique, en descendant de quinte en quinte, on génère SIb, MIb, LAb, RÉb, SOLb. Le SIb se positionne entre LA et SI en créant 2 demi-tons inégaux. L'intervalle entre SIb et SI est également un demi-ton chromatique (grand) et l'intervalle entre LA et SIb est diatonique (petit).
Calcul de l'intervalle SI♭-SI: SI♭1 vaut: (2/3)2 = 4/9 (tableau IV) donc SI♭3 vaut 16/9. L'intervalle entre SI♭3 et SI3 (243/128) sera: (243/128)/(16/9) = 2187/2048 ou 37/211
Des notes diésées et des notes bémolisées se trouvent intercalées dans le même ton à des endroits différents. Par exemple, entre le FA et le SOL, on a le FA# et le SOL♭. Ces deux notes sont très proches, mais ne se superposent pas. Le SOL♭ est le plus bas et le FA# est plus haut d'un tout petit intervalle appelé comma pythagoricien.
Le comma vaut 312/219 = 23,45 cents. C'est la différence entre le demi-ton chromatique et le demi-ton diatonique.
Calcul de l'intervalle SOLb-FA#: On connaît FA#: 36/29=729/512.
Pour déterminer SOLb3, on descend de quinte en quinte à partir de FA2: SIb1,
MIb1, LAb-1, RÉb-1, puis SOLb-2,
qui a pour rapport de fréquence (2/3)6=64/729. Pour SOLb3 on remonte de 4 octaves en multipliant par 24. Une autre façon est de descendre le SOL (3/2) d'un demi-ton chromatique (37/211). Dans les deux cas, on obtient le même résultat: SOLb: 210/36=1,4047.
En faisant le rapport des deux (36/29)/(210/36),on obtient 312/219.
La gamme de Zarlino comportant un demi-ton de 112 cents entre SI et DO, il est possible de le reporter dans le ton pour le partager en deux demi-tons inégaux. Cependant, comme il y a deux sortes de tons, l'un majeur (DO-RÉ) et l'autre mineur (RÉ-MI), il y aura deux façons d'effectuer ce partage.
Le grand ton de 204 cents se partage en 112 + 92
Pour le petit ton de 182 cents se partage en 112 + 70
On y voit donc 3 demi-tons différents, de 70, 92 et 112 cents.
Avec ses deux tons et trois demi-tons, cette gamme est complexe. Historiquement, elle a été abandonnée au profit des systèmes de tempéraments mésotoniques.
Au premier abord, ces préoccupations sur la définition des intervalles paraissent bien cérébrales et loin de l'interprétation musicale. Pourquoi tous ces calculs? Le musicien qui joue sa gamme ne s'imagine généralement pas que la définition des notes suscite tant de questionnements. Rendons-nous donc sur le terrain de la sensibilité musicale et de la beauté sonore pour découvrir si ces définitions d'intervalles peuvent intervenir, où et dans quelles circonstances.
Voici ce qu'a écrit le pédagogue E. Willems (voir article Puissance thérapeutique des sons):
Plusieurs théoriciens ont cru pouvoir expliquer la gamme par un seul système, celui de la quinte par exemple. Mais tous ceux qui ont un tant soit peu approfondi les multiples problèmes de la vie se rendent compte que la gamme est un ensemble très complexe d'éléments divers. Il ne suffit donc pas d'avoir recours exclusivement aux gammes grecques, à des calculs sur les vibrations sonores ou à un rapport unique de quinte pour expliquer sa formation... Lorsque l'être humain chante la gamme, il met à contribution des éléments de trois domaines nettement différents et cela simultanément: 1) la sensibilité physique par laquelle il sent les consonances, les dissonances et les écarts quantitatifs des intervalles; 2) la sensibilité affective, émotive qui lui révèle la valeur qualitative et expressive des intervalles; 3) l'intelligence, l'esprit d'analyse et de synthèse qui lui donne le sens harmonique (extrait de L'oreille musicale).
Lorsque l'artiste chante, il emploie souvent d'instinct une justesse expressive, différente de la justesse naturelle (celle de la gamme naturelle ou de la gamme de Pythagore) et de la justesse tempérée (gamme tempérée). La justesse expressive accentue le caractère attractif, appellatif (ou résolutif) de la note naturelle afin de lui donner une valeur caractéristique bien déterminée, mais variable selon les cas (E. Willems).
Ainsi de SI à DO, le demi-ton se réduit parfois à un quart de ton dans certains contextes expressifs, soit parce que le SI est attiré par le DO en DO majeur, soit parce que le DO est attiré par le SI, en LA mineur.
Le réglage est choisi afin de servir au mieux les intentions des compositeurs et des interprètes. Mais celles-ci varient et reflètent la mentalité de leur époque.
Il y a, comme dans le cas de Pythagore, l'aspiration à être en harmonie avec le cosmos, ou avec les lois divines, ou encore avec celles de la nature.
Au Moyen-Âge, l'adoption du système de Pythagore basé sur les quintes correspond à la musique de ce temps, car elle emploie essentiellement des quintes et des quartes. Ce sont des intervalles justes, c'est-à-dire, comme on l'a vu, dans un rapport harmonique (ou épimore).
Lorsque se répand l'usage de la polyphonie au 16e siècle, les compositeurs donnent une plus grande importance à la tierce majeure (par exemple DO - MI). Celle de la gamme pythagoricienne est trop grande. Lorsqu'on veut jouer les deux notes ensembles, des battements gênants du volume sonore se produisent. Aussi, dans la gamme de Zarlino, la tierce majeure DO-MI est réduite pour être ajustée.
Qu'est-ce qui a conduit ensuite à l'adoption de la gamme à tempérament égal dans notre civilisation des 19e et 20e siècles? Réponse: des considérations techniques de lutherie en lien avec l'évolution tonale de la musique.
Changer de tonalité, pour un mode donné, par exemple le mode majeur, c'est changer la hauteur à laquelle on le produit. Par exemple, pour une mélodie qui commence par DO en DO majeur, on la monte en commençant par un RÉ et on passe en RÉ majeur. Pour les instruments à sons fixes comme le piano, cela pose un problème concret.
Si le piano est accordé selon le système de la gamme tempérée, transposer la mélodie revient seulement à un glissement des intervalles. Il est relativement facile de décaler les mélodies d'un nombre quelconque de tons et demi-tons vers le haut ou vers le bas. On retrouve exactement le même air et tout va bien. C'est pourquoi ce système est bien adapté aux musiques des 19e et 20e siècles qui ont abondamment utilisé les changements de tonalité au point même de faire perdre la notion de tonalité dans la musique contemporaine (voir article Évolution de l'expression musicale occidentale: polyphonie et tonalité).
Cela ne se passe pas aussi simplement dans les autres systèmes de gammes puisque les demi-tons n'y sont pas égaux. Pour le démontrer, examinons ce qui se passe dans le cas de la gamme de Zarlino lorsqu'on transpose une mélodie de DO majeur à, par exemple, une tonalité de LA majeur.
Soit une mélodie qui commence par une quarte DO - FA (au hasard, La Marseillaise!, en FA majeur). Que se passe-t-il si je veux la jouer plus haut, à partir de MI ou de LA par exemple?
Les intervalles de quartes comportent deux tons et demi, mais dans la gamme de Zarlino il y a des grandes quartes et des petites quartes selon que les tons sont petits ou grands. L'intervalle de quarte DO-FA, qui vaut 4/3=1,333, est fait d'un grand ton T, d'un petit ton t et d'un demi-ton d (tableau VI). Si j'évalue cet intervalle de quarte à partir des autres degrés du mode, je trouve de même 4/3 pour RÉ-SOL, MI-LA, SOL-DO, SI-MI. Donc le début de ma mélodie ne changera pas si je la joue à partir d'un MI. Mais si je la joue à partir d'un LA, la quarte sera plus grande, car la quarte LA-RÉ est faite de 2 grands tons et un demi-ton TTd (1,350). Donc si je joue La Marseillaise à partir d'un DO puis d'un LA sur un piano accordé selon les valeurs de Zarlino, elle ne sonnera pas pareil dans les deux cas.
C'est pourquoi, si je veux transposer la quarte sur le LA (LA - RÉ) en conservant la même sonorité que sur le DO (DO - FA), je dois disposer d'une deuxième touche pour le RÉ, plus basse que la touche normale. Il faudra un clavier qui comporte deux touches pour le RÉ.
Or je n'ai considéré pour le moment que les quartes. Imaginez ce que ce sera si on considère tous les intervalles. C'est colossal! Examinons les quintes (voir tableau VI). La quinte DO à SOL est faite de TTtd de valeur 1,5, alors que la quarte RÉ-LA est plus petite avec Tttd de valeur 1,48. Il me faudrait donc également 2 touches pour le LA. Examiner les tierces serait également instructif. Je vous en laisse le soin.
À partir du 16e siècle, on a tenté de construire des instruments à clavier qui avaient un nombre plus important de touches, avec des touches dédoublées pour les notes proches l'une de l'autre d'un comma, par exemple un DO# et un RÉb. L'archicembalo de Nicola Vicentino (compositeur italien, 1511 - 1575) comportait 36 touches dans l'octave qui produisaient 32 notes différentes. Mais cela complique beaucoup le jeu de l'interprète, et cela n'a pas perduré.
Toutefois, à cause du besoin actuel de retrouver une intonation juste, cette recherche est à nouveau bien vivante, avec une approche différente et une technologie plus puissante. Ainsi, le guitariste D. Aschour joue sur une guitare dont le manche possède des frettes interchangeables.
Décaphone Surak-Nat-Buzurg de Jacques Dudon (1997)
pour le guitariste Didier Aschour
L'autre solution est de faire des compromis: abandonner l'idée de touches multiples et ne conserver que 12 notes dans la gamme chromatique, donc confondre DO# et RÉb. C'est accepter de jouer avec une intonation moins juste. Dans ce cas, comme je l'ai montré plus haut, le changement de tonalité sera accompagné d'un léger changement de grandeur des intervalles.
Or si j'attribue à deux notes très proches la même touche, à quelle valeur vais-je l'accorder? Je vais choisir une moyenne entre ces notes. Les différentes façons de choisir cette moyenne pour chacune des 12 notes d'une gamme constituent les tempéraments.
On doit s'arranger pour que la modification d'intervalle lors d'une transposition soit la moins perceptible possible. Comment conserver sa valeur dans toutes les tonalités? Le problème est que si on conserve cette valeur pour les intervalles d'octave, on ne pourra pas le réaliser simultanément pour les quintes, encore moins pour les tierces. Il faut choisir ce qu'on met en priorité et cela dépend du style de musique.
Le dilemme entre le respect de la justesse des octaves et celui de la justesse des quintes se pose mathématiquement de la façon suivante. Si on monte de quinte en quinte, comme on l'a fait dans la gamme pythagoricienne, en conservant le même intervalle de quinte juste (3/2), on génère les 12 notes chromatiques. Par exemple, en partant du Mi♭, on arrive au SOL#. En avançant d'une quinte supplémentaire, on génère la 13e note qui est RÉ#. C'est donc la même que la première, Mi♭, 7 octaves plus haut... mais pas tout-à-fait. Car le RÉ# est très légèrement plus haut que le Mi♭.
En effet, la douzième quinte nous amène à la valeur (3/2)12 =129,75 pour le RÉ#, alors que la septième octave nous amène à 27=128 pour le Mi♭. Le cycle des quintes nous mène un peu plus haut que le cycle des octaves. L'intervalle Mi♭-RÉ# vaut donc 312/219 en rapport de fréquences. C'est le comma pythagoricien que nous avons rencontré plus haut. En fait, c'est l'origine de ce comma, son acte de naissance.
Le douzième quinte, l'intervalle SOL# - Mi♭ est une quinte raccourcie, donc fausse à l'oreille, qui pour cette raison a été nommée quinte du loup.
Comment concilier ces deux cycles dans l'accord d'instruments à sons fixes où le nombre de touches est limité à 12? Il existe plusieurs types de réponses, qui définissent plusieurs types de tempéraments.
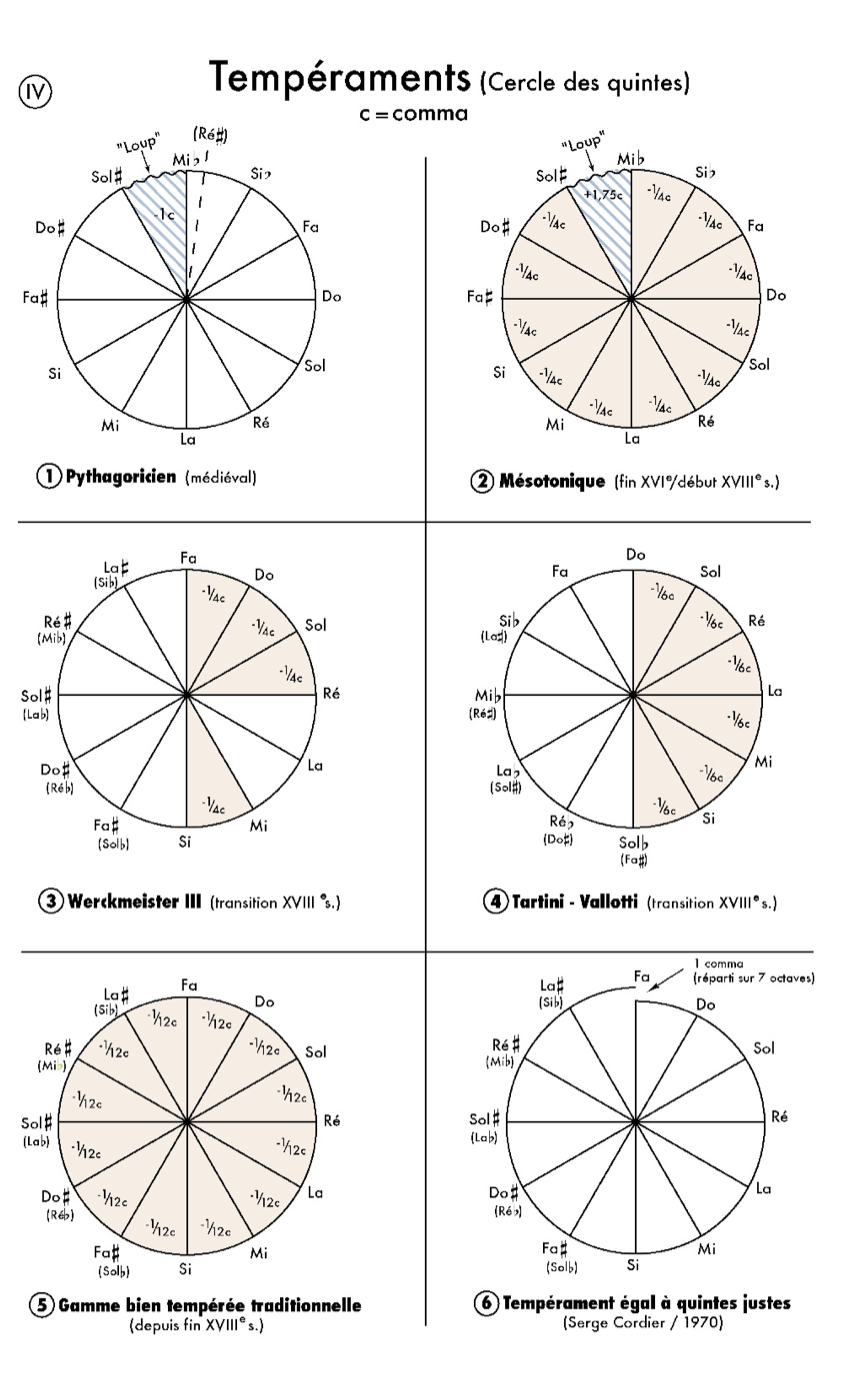
Tableau du cycle des quintes dans les différents tempéraments historiques.
Extrait de Tempérament, Glossaire, par Serge Cordier
Qu'est-ce donc qu'un tempérament? Le tempérament, c'est la manière de répartir cette différence d'un comma sur l'ensemble des notes, de façon équilibrée sur tous ou partie des intervalles, de sorte que les octaves restent justes et que les quintes, puis les tierces, puis les intervalles d'harmoniques supérieures, le soient le plus possible. Nous verrons qu'on peut aussi partir des quintes justes ou des douzièmes justes et adapter l'octave en conséquence.
Dans le système à tempérament égal qui prévaut actuellement depuis la fin du 18e siècle, le comma est réparti de façon égale sur toutes les notes. La quinte s'en trouve donc diminuée de 1/12e de comma soit environ 2 cents, et la tierce augmentée, comme on l'a vu dans le tableau récapitulatif.
Toutefois, rien n'impose que cette répartition soit homogène. Plus d'une centaine de types de tempérament inégal ont été proposés depuis le 11e siècle et jusqu'à aujourd'hui. C'est dire combien cette question a préoccupé les compositeurs et facteurs d'instruments, sans commune mesure, par exemple, avec le choix d'un diapason qui agite certaines franges de notre société actuelle (voir l'article La hauteur des notes de musique doit-elle être normalisée par un diapason (LA 440, LA 432 ou autre)?)
Dans les tempéraments inégaux, le comma de trop est réparti sur 4 ou 6 notes, au lieu des 12 du tempérament égal (voir le tableau ci-dessus). Le tempérament qui prévalait au 16e siècle, le tempérament mésotonique, mettait l'accent sur la tierce. La tierce DO - MI apparait comme la succession de 4 quintes. Afin qu'elle sonne juste, ces quintes ont été abaissées de 1/4 de comma.
Ainsi, lorsque Bach écrivait pour le clavecin "bien tempéré", il ne parlait pas de tempérament égal, mais de tempéraments inégaux qui permettaient de jouer dans de nombreuses tonalités et qui avaient sa faveur (pour les spécialistes: les discussions sont actives à ce sujet, mais elles convergent pour proposer les systèmes de Werckmeister III ou Kirnberger II ou proches d'eux).
Puisque les quintes et les tierces, dans un tempérament inégal, sont inégales, des airs sonnent différemment selon qu'ils sont interprétés dans une tonalité ou une autre. Cela explique qu'on attribuait à chaque tonalité un caractère, une ambiance différente (l'éthos). Ce n'est pas le cas avec une gamme tempérée où toutes les tonalités sont identiques. Toutefois certains, rares, affirment qu'ils distinguent des ambiances différentes selon les tonalités, même en tempérament égal, mais on ne comprend pas pourquoi.
Pour plus de détails sur les différentes sortes de tempéraments, se reporter à des articles plus techniques, par exemple: La justesse musicale, conférence de Serge Cordier, 1991; Les tempéraments par Marc Texier, consulté aout 2016; Musique et tempéraments par Didier Guiraud de Willot; Gammes et tempéraments, Wikipedia
À la fin du 18e siècle, la gamme à tempérament égal a supplanté les tempéraments inégaux comme une solution (il y en aurait d'autres possibles) pour répondre au problème pratique de changement de tonalité qui devenait crucial pour les instruments à clavier. C'est l'époque du succès de la modulation, de la transposition et de la polyphonie instrumentale. Elle évite d'ajouter des touches aux 12 courantes tout en faisant en sorte que les quintes ne soient pas trop diminuées pour que cela soit directement perceptible.
À ce stade de notre exposé, il est nécessaire d'introduire 3 nouveaux éléments qui interviennent pour apprécier la justesse d'un intervalle de deux notes. L'un est l'existence de battements, l'autre celle de partiels et le dernier l'imprécision de nos perceptions auditives.
Le son est physiquement une onde qui se propage dans l'air. Aussi lorsque nous émettons simultanément deux sons de fréquences définies différentes, les ondes vont se combiner, se renforcer en certains points, s'atténuer à d'autres (voir mon article Physique et perception du son). Lorsque les fréquences des ondes ont des valeurs proches, elles interfèrent et il se crée des battements. Le volume du son passe périodiquement par des forts et des faibles qui sont bien perceptibles à l'oreille. On calcule que si les fréquences des 2 ondes diffèrent de 1 Hz (1 vibration/s), le battement créé se répète toutes les secondes. En effet, le nombre de battements par seconde est égal à la différence des fréquences des deux ondes. Donc plus les deux fréquences se distancient et plus les battements deviennent rapides.
Or une note émise par un instrument n'est pas composée seulement d'une seule fréquence (par exemple un Do2 de 130 Hz). Elle est la superposition de la fréquence fondamentale et de ses harmoniques, double, triple, quadruple, quintuple, etc (harmonique 2 à 260 Hz - DO3, harmonique 3 à 390 - SOL3, harmonique 4 à 520 - DO4, harmonique 5 à 650 Hz - MI4...). (Voir l'article Timbre
et harmoniques; sur la numérotation des octaves DO2, DO3 etc., voir l'article Son:
hauteur et fréquence)
Par conséquent, lorsque deux notes sont émises simultanément par un instrument qui le permet (claviers, guitare, luths), les interférences se produisent non seulement entre leurs fréquences fondamentales, mais également entre les harmoniques de l'une et le fondamental et les harmoniques de l'autre.
Ainsi si nous jouons un DO3 et un SOL3, l'harmonique 3 du DO3 (SOL4) interfère avec l'harmonique 2 du SOL3 (le même SOL4). Si l'harmonique 2 du SOL3 a exactement la valeur de l'harmonique 3 du DO3, on dit que l'intervalle est pur. On ne perçoit (en principe) pas de battements. Pur signifie que l'intervalle a exactement la proportion mathématique harmonique. Si les deux SOL4 sont ajustés plus haut ou plus bas, alors des battements se produisent.
Pour un musicien, ces battements peuvent être gênants s'ils sont trop marqués. Mais s'ils sont lents, ils peuvent au contraire donner du relief au son. Par exemple, une octave telle que DO3 de 130 Hz à DO4 de 262 est agrandie de 2 Hz par rapport à l'octave pure. Mais elle peut sembler tout à fait juste à l'oreille et plus agréable que l'octave pure.
Or, dans le cas des instruments à cordes (piano, violon, guitare), les harmoniques émises par une corde vibrante ne sont pas exactement harmoniques, car leurs fréquences sont un peu plus que le double, le triple ou autre multiple de la fréquence fondamentale. Cela est dû au fait qu'une corde matérielle a une épaisseur et une rigidité. C'est le phénomène d'inharmonicité, mis en évidence il y a quelques dizaines d'années, après l'invention d'appareils qui permettent des mesures précises des fréquences (voir à ce sujet l'article Histoire de la notion de fréquence sonore). Les harmoniques qui n'en sont plus vraiment reçoivent le nom de partiels. L'inharmonicité du piano est surtout sensible dans les aigus, faible dans le médium, et perceptible dans les basses.
En conséquence, dans le cas du piano par exemple, l'explication précédente sur le phénomène de battements doit être corrigée en remplaçant les harmoniques par les partiels, légèrement plus hauts que les harmoniques. Un accordeur de piano accorde les cordes en écoutant les battements entre les partiels réels et non entre des harmoniques théoriques. De ce fait, lorsque l'octave sonne sans battement, elle est un peu dilatée par rapport à l'octave pure, tout en sonnant parfaitement juste.
On évalue la précision d'un intervalle à l'oreille ou avec des instruments de mesure. Dans les deux cas, la précision n'est pas absolue. Toute mesure dans la matière, que ce soient une distance, un poids, un temps, est réalisée à une certaine tolérance près. Ainsi vous évaluerez un temps de trajet en voiture en heures et en minutes mais vous omettrez les secondes. Et si vous évaluez la durée d'une vidéo en minutes et secondes, vous omettez les millièmes de secondes.
Dans le cas de l'oreille, intervient de plus sa limite de perception. Si des battements sont trop rapides, vous ne percevez plus chacun des battements, mais un ronflement continu. S'ils sont trop lents, on ne les perçoit plus non plus. C'est pourquoi, lorsqu'un accordeur se fie aux battements des partiels pour réaliser ses accords, il le fait à une toute petite tolérance près. La sensation de battement s'annule en effet en dessous de 0,3 battements par seconde dans le médium.
Tous les tempéraments exposés précédemment, inégaux ou égal, restent accrochés à la définition d'un intervalle d'octave pure. L'octave fait partie de la nature, donc elle semble intouchable, définitivement attachée au chiffre 2 connu depuis l'antiquité (voir article La hauteur des notes de musique doit-elle être normalisée par un diapason?).
Serge Cordier, inventeur du tempérament égal à quintes justes.
Merci au site web Tempérament Cordier
À l'opposé, il revient à l'accordeur et théoricien Serge Cordier (1933 - 2005) d'avoir proposé en 1972 de conserver la justesse de la quinte et de relâcher la contrainte du 2 pour l'octave. De longues études et expérimentations l'ont amené à inventer le tempérament égal à quintes justes pour l'accord des pianos et des claviers.
Puisque la 7e octave est plus basse d'un comma que la 12e quinte, il suffit d'augmenter chaque octave de 1/7e de comma, soit 3,35 cents, pour être en accord avec les quintes justes (voir tableau des quintes ci-dessus). C'est ce que fait Cordier, puis il égalise les 7 demi-tons contenus dans une quinte (tempérament égal).
L'idée de ce tempérament lui est venu à la suite de ses analyses des pratiques des accordeurs de piano. De même, les violonistes règlent leurs instruments par quintes justes, car les cordes sont espacées de quintes: SOL - RÉ - LA - MI. Autrement dit, Cordier, comme il le disait lui-même, a découvert ce qui existait déjà et l'a théorisé, développé, en a exploré les qualités et a montré ses avantages sonores par rapport au tempérament égal à octaves justes.
Il s'est aperçu que l'oreille non seulement n'est pas dérangée par la dilatation minime de l'octave, mais que de plus elle l'appréciait. Pour le musicien, cette dilatation est parfois musicalement plus juste que l'octave physique naturelle. La tendance spontanée des musiciens qui sont libres de la hauteur de leurs notes est souvent d'agrandir légèrement certains intervalles, surtout dans l'aigu. Les octaves supérieures, lorsqu'elles respectent la mathématique du 2, paraissent plutôt trop basses. Il semble que ce soit dû à la fois à une influence culturelle et au fonctionnement perceptif de l'oreille qui n'est pas linéaire. Autrement dit la justesse expressive musicale ne se confond pas avec la justesse naturelle.
Cela rejoint les résultats de recherches en acoustique musicale des scientifiques français Émile Leipp (1913 - 1986, Laboratoire d'Acoustique Musicale) et Jean-Claude Risset (1938 - 2016, IRCAM) également compositeur, qui ont montré indépendamment que la sensation de hauteur des notes et d'intervalles n'était pas directement liée à la physique, mais dépendait de façon complexe de facteurs psycho-affectifs. Les mesures effectuées sur la pratique vivante des musiciens révélèrent que les intervalles réels produits sont différents des intervalles supposés de la théorie physique. Ils se raccourcissent ou s'agrandissent selon le contexte musical et la sensibilité de l'acteur. Pour l'accord des pianos, Leipp rapporte que Les notes de l'octave la plus grave étaient "trop basses" d'un bon quart de ton; les notes les plus aigües [...] trop hautes d'un demi-ton. (Réunion du GAM, décembre 1978), du moins en comparaison des valeurs pures théoriques.
Cordier a reçu des témoignages élogieux sur son accordage de piano, quelquefois de la part de musiciens célèbres, dont Yehudi Menuhin. Les musiciens ont fait part de leur satisfaction car le son est plus pur, plus rond, plus vivant et gagne en luminosité.
Plus de détails sur Internet: Le tempérament Cordier, un nouvel accord des pianos. Voir en particulier la conférence de 1991 La justesse musicale, le glossaire.
Toutefois, ces qualités sont perçues surtout dans la mélodie, c'est-à-dire lorsque les notes sont jouées successivement. Lorsqu'on les joue simultanément, dans des accords plaqués, des inconvénients acoustiques peuvent apparaitre (battements trop marqués) pour des notes distantes de 2 ou 3 octaves. Pour atténuer ou éliminer cet inconvénient, d'autres systèmes ont été recherchés, intermédiaires entre le tempérament égal d'octave et celui de quinte.
Je suis redevable aux études approfondies d'André Calvet, accordeur et technicien de piano, enseignant à l'Institut technologique européen des métiers de la musique au Mans (ITEMM), pour les informations de cette partie et des précisions sur les parties précédentes (voir son ouvrage, Le clavier bien obtempéré). Calvet attire l'attention sur l'intérêt du tempérament égal à 12e pures de Bernhard Stopper et du Circular Harmonic System d'Alfredo Capurso. Il propose lui-même un tempérament de son cru, le Clavier Bien Obtempéré (CBO).
Bernhard Stopper, pianiste et facteur de piano allemand, né en 1961, énonce son tempérament dès 1988. Il s'appuie sur l'intervalle de douzième pure, addition d'une octave et d'une quinte. Il est divisé en 19 demi-tons égaux. Stopper a développé un logiciel pour l'accord du piano (Tunic OnlyPure).
Alfredo Capurso est un technicien et accordeur de piano italien vivant à Londres. À partir de 2007, il a développé un tempérament personnel, le Circular Harmonic System ou C.ha.s, adapté au piano pour tenir compte des partiels (de l'inharmonicité) de façon flexible. Il est proche du précédent tout en se rapprochant du tempérament égal. Les octaves en sont donc étirées. Tous les intervalles sont calculés pour avoir une tension satisfaisante à l'oreille. A. Calvet affirme avoir été séduit par le son obtenu avec ce tempérament lors d’une démonstration à l’ITEMM (ampleur, chaleur, richesse sonore).
Plus de détails sur Internet: Piano Stopper Tübingen. On y trouve une publication théorique, Tuning
The Stopper Equal Temperament With The Tunic PDA Software, 2008. Exemple sonore joué par Grigory Sokolo Piano
Technicians Guild Convention 2011; vidéo explicative du système d'accord
un texte explicatif de la pratique de l'accord en C.Ha.s; la publication de base;
un cours en anglais sur les intonations
André Calvet (son site web expose ses recherches et ses publications dans une variété de domaines) a été amené à élaborer une nouvelle pratique de l'accord du piano qui repose sur la sensibilité de l'écoute et non sur des rapports mathématiques précis. C'est donc plutôt une méthodologie, qu'il nomme lui-même une prathéorie, autrement dit une théorie qui se modifie selon la pratique réelle, incluant le piano, l'accordeur et le concertiste. Elle est fondée sur l'écoute des battements des intervalles entre partiels. Elle inclut donc la tolérance d'environ 0,3 battements en-dessous de laquelle l'oreille ne les perçoit plus (dans le médium).
A. Calvet a malicieusement nommé cette prathéorie le Clavier Bien Optempéré (CBO) qu'il a traduit en anglais par Well Optimized Keyboard ou WOK.
Elle se situe entre le tempérament égal à octaves pures, souvent jugé plat, et le tempérament égal à quintes justes, qui est perçu comme trop tendu. La différence principale est que les battements d’octave, de douzième et de quinte ne sont pas déterminés à l’avance, car les battements réels peuvent varier d'un piano à l'autre. L'accord respecte les caractéristiques de l’instrument, la personnalité de l’accordeur, et les vœux éventuels du commanditaire.
En ne faisant pas coïncider à la perfection les partiels concernés [par les octaves et les quintes], nous éprouvons à l’écoute de ces deux intervalles une sensation de pur, enrichie par un caractère plus chaleureux, moins strict, plus libre. A. Calvet, communication privée
Je
signale également une réalisation informatique intéressante qui permet de « matérialiser » sous forme sonore de nombreuses échelles et tempéraments : c'est le clavier numérique ci-contre, nommé Sémantic Danielou-53, mis au point par Jacques Dudon, en collaboration avec Arnaud Sicard et Christian Braut, téléchargeable gratuitement sur le site.
Selon leurs auteurs, le but est de rendre accessible au plus grand nombre l'expérience de l'intonation juste à travers de nombreux modes pré-programmés issus de l'échelle globale du Semantic : ragas indiens, échelles de diverses cultures musicales, démonstration des différents commas, tempéraments schismatiques, linéaires et fractals reliés au système Semantic. Cela passe donc par un système de fréquences électroniques ajustables, calculées précisément selon la valeur des intervalles en fraction.
Finalement, l'enjeu de tout cela n'est-il qu'un problème pratique de lutherie? Non. La question bien plus cruciale est que l'utilisation de la gamme tempérée a habitué notre oreille à cette intonation, au point que des musiques exécutées dans d'autres systèmes peuvent nous sembler fausses.
Le problème est donc plus profond que la mise au point de dispositions pratiques concernant la fabrication des instruments. Il est relié à notre sensibilité auditive vis-à-vis des subtilités des intervalles. Il est dans le choix d'un univers sonore. Il est dans la question de l'incidence de cet univers sur notre bien-être.
Le physicien Helmholtz, promoteur de la gamme naturelle de Zarlino, indiquait combien la musique ancienne était altérée par la gamme tempérée. Les particularités de la gamme naturelle se manifestent surtout dans l'ancienne musique italienne de Palestrina, Vittoria, Gabrieli et leurs contemporains. Ces œuvres réclament les consonances les plus justes parce qu'elles n'obtiennent les nuances les plus délicates de l'harmonie que par le renversement des accords, l'alternance des accords majeurs et mineurs, et un petit nombre de dissonances formées par des retards. Exécutées dans la gamme tempérée, elles perdent tout sens et toute expression, tandis que, grâce à l'emploi de la gamme naturelle, elles produisent sur l'harmonium un bon effet (Helmholtz, cité par O. Bettens).
On pourrait penser que l'interprétation dans la gamme tempérée ne concerne pas le chanteur, qui peut ajuster sa voix à toutes sortes d'intervalles à volonté. Il peut commencer sa mélodie sur n'importe quelle note et conserver tous ses intervalles justes par glissement. Il en est de même pour les instruments à cordes sans frettes tels que les violons. Toutefois, les interprètes sont plongés dans la culture de la gamme tempérée, sont accompagnés d'instruments à sons fixes, et leurs oreilles sont conditionnées. Aussi, continue O. Bettens, Helmholtz ajoute que les chanteurs sont incapables de chanter "de manière à donner à l'auditeur ce bien-être complet qui résulte d'une parfaite harmonie", ce qu'il attribue à l'influence néfaste des pianos accordés au tempérament égal avec lesquels ils s'exercent.
De son côté, au cours de ses recherches sur l'interprétation du chant chrétien antique, le chercheur et musicien Iégor Reznikoff a fait l'expérience d'un déconditionnement total de l'oreille. D'excellents musiciens restent perplexes quand on leur dit que l'accord actuel du piano est faux, et qu'on le leur fait entendre. J'en ai fait personnellement l'expérience quand je me suis mis à travailler la musique antique et le répertoire occidental ancien. Pour mieux approcher cette musique, j'ai non seulement arrêter de jouer du piano et de faire des concerts de musique de chambre ou de chanter dans des chorales, mais pendant longtemps je me suis abstenu d'écouter de la musique occidentale, n'écoutant que des musiques dont on peut être sûr quant à la rigueur de la transmission orale, de la musique sacrée au sens strict du terme et remontant aux traditions les plus anciennes - la nuit des temps - et sur lesquelles, en tout cas, aucune musique récente n'avait eu d'influence. Je n'écoutais que de ces musiques et ne travaillais que la résonance harmonique d'une corde. Alors peu à peu, au bout de neuf mois de cette ascèse, l'oreille se déconditionne, une physiologie plus fine réapparaît, un nuage se lève, on peut entonner des intervalles justes, les varier d'un comma... Ce fut avec la très célèbre Symphonie en sol mineur n°40 de Mozart que je repris contact avec la musique occidentale. Expérience inoubliable, tout me parut faux d'un bout à l'autre..." (I. Reznikoff, Entrer dans la résonance).
La musique contemporaine s'est complètement affranchie de la définition classique d'un mode. Il devient permis de sélectionner n'importe quel son du continuum sonore et d'inventer tous les intervalles possibles (voir article Évolution de l'expression musicale occidentale: polyphonie et tonalité). C'est comme si les échelons, auparavant bien marqués sur l'échelle de l'octave évoquée au début de l'article, avaient été remplacés par des crochets coulissants qu'on peut insérer où l'on veut et avec le nombre qu'on veut. Cette recherche est très facilitée par des appareillages électroniques où les caractéristiques des sons, hauteur, volume, timbre, dynamique, sont ajustables à volonté (voir article Sensations sonores).
Nous ne sommes pas contraints à l'emploi de la gamme tempérée et nous pouvons libérer notre esprit des habitudes et des idées toutes faites. Il était probablement nécessaire que les compositeurs poussent la recherche et l'audace jusqu'à l'éclatement de la gamme tempérée, afin de faire germer une nouvelle connaissance et une conscience accrue du monde sonore.
Cependant, à cette phase d'acquisition de liberté, en succède une autre, celle du choix. Faire éclater les coquilles de l'ancien, d'accord, mais pour construire quel monde?
Le choix d'un tempérament n'est pas réductible au problème d'accord instrumental qui lui a donné naissance. Le choix d'un tempérament est le choix d'une échelle sonore. C'est l'acte primordial par lequel les musiciens établissent une collection de sons discontinus prélevés dans un continuum sonore qui nous entoure, ensemble de sons que régit une loi mathématique. C'est le premier moment de l'organisation musicale, l'instauration d'un paradigme harmonique, dont toute la musique ensuite est dérivée (M. Texier).
Un exemple quasi-général de confusion a comme origine les micro-intervalles générés par différentes coïncidences naturelles inévitables entre les harmoniques, de type comma... Avec les notes doubles qu'ils mettent en valeur, il importe de pouvoir en discerner l'existence, la place et le rôle dans toute échelle musicale. La négation de ces commas recherchée pour limiter le nombre de notes par octave d'un système simplifie les instruments et le jeu instrumental, mais a pour effet un appauvrissement harmonique du modèle naturel et une perte de son sens et de sa résonance... La confusion ici ne vient pas des musiques, mais de l'incapacité de certains théoriciens, à certaines époques, à rendre compte des réelles pratiques des musiciens ou à saisir la complexité naturelle des relations harmoniques entre les sons, enfin des luthiers à faire des instruments nécessaires pour créer de meilleures situations d'écoute et de transmission... Il ne peut y avoir en même temps simplification de la division de l'octave et consonance, c'est-à-dire simplicité harmonique. Tout système d'intonation propose un choix. C'est l'éternel débat entre les pythagoriciens et les aristoxéniens, entre le son et la forme, la justesse et l'orchestration, la modalité et la modulation, le timbre et la virtuosité, la tampura et le clavier, l'Orient et l'Occident... Là où il y a confusion, c'est aussi parce qu'il existe des passerelles entre différents mondes, et donc une harmonie potentielle.. (J. Dudon: La confusion des genres: tentatives de résolution, Colloque "Autour de l'harmonie", Carcès, France, 15-16/10/2004).
Lorsqu'elle fait l'expérience du silence, l'oreille retrouve une sensibilité accrue qui lui permet d'entrer dans des mondes plus subtils. Il est alors plus facile de sentir et de discerner ce qui fait du bien ou ce qui agresse et dérange. Et l'on peut constater que parfois, lorsque les êtres humains se sont coupés de leur nature profonde, et qu'ils ne sont plus reliés au cœur et au corps comme cela se produit dans la civilisation occidentale contemporaine matérialiste, l'expérimentation peut accoucher de monstruosités. Certaines musiques morcellent et détruisent les personnes. D'autres musiques harmonisent et réunifient l'être. Elles sont accordées aux lois physiologiques et psychiques qui ne dépendent pas de la culture, mais sont inscrites profondément dans la constitution de l'être humain, elle-même construite selon des lois cosmiques (voir article Les corps subtils et les chakras).
La vérité est dans la résonance intérieure. La résonance avec notre cœur, notre âme, et notre corps.
Lorsqu'un théoricien propose un nouveau monde sonore, celui-ci ne se développe et ne se répand que s'il plait, s'il procure une jouissance, autrement dit s'il résonne avec notre être intérieur. Or il n'y a pas que l'oreille qui perçoive les sons, car le corps les reçoit, les enregistre et réagit même si l'oreille ne perçoit pas. Dans l'eau, on entend parfaitement les sons même en se bouchant les oreilles, expérience que propose F. Louche dans sa recherche sur l'écoute active. Or ces sons s'étagent à des endroits précis du corps et agissent sur les circuits nerveux et les organes (voir article Résonances sonores corporelles).
Certains, tels Pythagore, Platon, Képler ou le Rig Veda indien, ont démontré les rapports de la musique avec le cosmos. Leur quête était de créer une musique qui soit en accord avec l'être humain (le microcosme) et l'univers (le macrocosme). Le cosmos comme l'être humain sont bâtis selon des rapports privilégiés qui fondent ce qu'on appelle la géométrie sacrée (voir article Aspects géométriques de l'univers). C'est pourquoi l'homme se sent intuitivement relié à la nature, aux étoiles, à l'ordre universel.
Au siècle dernier, des théoriciens ont tenté de retrouver cette correspondance entre les notes et le cosmos de façon très concrète en utilisant les connaissances métriques de l'astronomie. Par exemple Derénéaz a étudié les distances des planètes au soleil (en prenant la moyenne entre le périhélie et l'aphélie) et leurs correspondances avec les fréquences des notes de la gamme majeure (dans La gamme, ce problème cosmique). Exemple: si l'on prend une corde sonore comme unité de longueur représentant la distance Soleil-Terre, et que l'on y place un chevalet correspondant aux distances Neptune-Uranus, Uranus-Saturne et Saturne-Jupiter, on obtient les intervalles DO-RÉ, MI-FA (plus de précisions dans le document Harmonie des Sphères). Cette correspondance me semble très mentale et alambiquée. Par exemple comment et pourquoi prendre la moyenne, pourquoi le périhélie et l'aphélie? Toutefois, il est probable que l'harmonie des sphères existe bel et bien, mais n'est plus perçue dans sa vraie dimension, qui se trouve à un autre niveau, plus vibratoire, plus symbolique. Ainsi certains yogis entendent des sons intérieurs, tout en ayant la sensation d'être unis au jeu de l'univers. On trouve l'univers en soi.
Oui, nous éprouvons le besoin de retrouver un nouvel espace harmonique, basé sur les résonances naturelles. Depuis quelques années, on revient à l'écoute des gammes naturelles. Le succès de la musique baroque reconstituée dans son authenticité, et celui des musiques extra-européennes y ont beaucoup contribué. Ce mouvement a également bénéficié de la vulgarisation du chant diphonique qui exploite le renforcement sonore des sons harmoniques (voir article Sensations sonores: timbre) et par les études dans l'interprétation musicale et vocale de pionniers tels que Iégor Reznikoff et Jacques Dudon:
Parlant de l'intonation juste, Paul Hindemith disait - affirmation remarquable pour un musicien du XXe siècle - que celui qui a le sens de cette intonation possède une dimension supplémentaire, et donc un compréhension autre de la Musique... Cette approche suppose une écoute autre, une perception fine que seules l'intonation et la consonance justes permettent. Il se passe alors des phénomènes à un niveau subtil dans la mesure où le son agit en des points précis du corps, sur des centres essentiels et sur la conscience profonde, suivant des circuits énergétiques à la perception desquels nous ne sommes pas habitués normalement (I. Reznikoff, L'intonation juste).
Le chant sacré - en rapport donc avec le monde de l'Esprit - dans toute sa vérité modale antique est bâti sur les principes de résonance naturelle et d'action des syllabes sur divers lieux du corps évoqués plus haut et développe ces principes de façon rigoureuse afin d'agir sur le son, science profonde, en transmettant, par leurs caractéristiques et impression sonore propres, des états de concentration, de contemplation, de prière, des états de paix, d'appel à Dieu, de joie de la Présence Divine, d'attente... suivant le temps et le moment liturgiques (I. Reznikoff, Musique grecque antique, byzantine et traditionnelle).
Willems synthétise l'ensemble de ces considérations: Notre gamme diatonique reste un mystère, malgré toutes les explications données. La raison en est qu'elle touche à la fois à des éléments cosmiques et humains. Voici les principaux facteurs qui ont influencé la constitution de la gamme:
Je ne prétends pas être un expert des gammes, mais plutôt un traducteur d'un domaine un peu technique, dans un langage abordable, si possible par le moyen de l'écoute et du ressenti. Il se peut qu'il subsiste des erreurs.
Si cet article a éveillé votre curiosité et que vous voulez en savoir encore plus, vous pouvez consulter les documents en ligne suivants:
17 janvier 2006 - ajout (tempéraments Cordier, Stopper, Capurso, Calvet) 31/08/2017 - dernière révision et ajout (Semantic-Danielou) 1/02/2021
