Aspects géométriques et sonores de l'univers
Alain Boudet
Dr en Sciences Physiques
Résumé: Loin d'être dues au hasard, les formes de l'univers sont sous-tendues par des trames géométriques. On constate leur présence depuis l'atome jusqu'aux amas de galaxies, en passant par les plantes, les animaux, les circuits énergétiques de la Terre, et même le corps humain. Ces géométries sont intimement liées à des fréquences sonores. Sons et géométries sont l'expression manifestée de schémas directeurs sous-jacents.
Contenu de l'articleLes scientifiques nous affirment que l'univers est né à partir d'un point microscopique qui a explosé dans un immense Big Bang. Au fur et à mesure que l'énergie de l'explosion s'est propagée, elle a occupé de plus en plus de volume. En même temps, sa température a décru, et sont apparues les forces fondamentales de la gravité et de l'électromagnétisme, puis les éléments de matière: particules, atomes, puis enfin étoiles et planètes. Sur une planète spéciale, la Terre, la vie s'est développée sous forme de bactéries, puis de plantes et d'animaux, et enfin d'êtres humains.
Dans cette évolution, ce qui aurait présidé à l'apparition des magnifiques formes de la matière et de la vie, c'est le plus pur des hasards. Au hasard des rencontres, des associations d'éléments se font et se défont. Les associations les plus fortes, les plus stables, et celles douées d'un pouvoir de croissance et de reproduction, auraient pris de la place au détriment des autres, par un mécanisme de sélection naturelle (voir article Les origines de la Vie).
Ce scénario n'est pas la transcription d'observations directes. C'est un modèle hypothétique, élaboré pour rendre compte des rudiments d'observations astronomiques que les astrophysiciens ont collectées depuis notre petit coin d'univers, la Terre, et son environnement spatial proche, avec nos instruments dont la technologie est admirable, mais limitée.
Les astrophysiciens adhèrent massivement à cette théorie. Ce qui surprend et nous interroge dans ce scénario, c'est comment une explosion brutale, sans finalité ou sans guide de conduite, aurait pu donner naissance à toutes les lois physiques minutieusement réglées de notre univers et à la profusion des formes de vie que nous observons. Les physiciens eux-mêmes ont été frappés par le fait que les constantes fondamentales de la physique (charge de l'électron, constante de la gravité, vitesse de la lumière, etc.) sont ajustées avec précision pour assurer les conditions de la vie. C'est ce qu'ils ont nommé le principe anthropique (à ne pas confondre avec le principe de l'entropie). Les formes de vie, qui font preuve d'énormes capacités d'adaptation aux changements dramatiques de l'environnement, nous démontrent à quel point elles sont régulées par d'extraordinaires mécanismes de fonctionnement. Tous ces phénomènes ne seraient-ils pas le fruit d'une intelligence? Ou tout au moins d'une science supérieure?
À ceux qui émettent des doutes sur la valeur de la théorie du Big Bang, les scientifiques répliquent que c'est la seule théorie valable et qu'elle est acceptée par tous. Ceux qui ne sont pas convaincus par l'emploi des lois du hasard, sont soupçonnés de réintroduire le principe du finalisme ou téléologie qui a été laborieusement abandonné au 19e siècle par les efforts de la science, et de faire appel à une intelligence créatrice (Dieu) dans leur scénario. Autrement dit, un opposant au scénario scientifique standard du Big Bang s'expose à être taxé de complicité avec le créationnisme, ce qui pour un scientifique est un manquement grave à la science. Les créationnistes prennent le texte biblique à la lettre sur le plan matériel, niant sa valeur symbolique. Selon eux par exemple, la Terre aurait été créée en 6 jours et serait âgée de 6000 ans.
En-dehors de ces deux positions extrêmes, le tout-hasard ou la création en 6 jours, n'y aurait-il pas d'autres voies envisageables, d'autres scénarios de création?
Le but de cette étude n'est pas de polémiquer sur l'opposition entre la théorie scientifique cosmologique actuelle et le créationnisme. Il est de proposer un autre regard, un autre type de scénario. Ce scénario n'est pas inventé à partir de rien. Il résulte de la convergence d'observations scientifiques concernant les aspects géométriques de l'univers, et d'enseignements traditionnels sur la description du cosmos et de sa création. Cette convergence nous amènera à une vision renouvelée de l'Homme et de son rapport avec le cosmos. C'est une vision cohérente, qui d'une part donne du sens aux mythes et aux légendes, et qui d'autre part redonne à l'Homme sa place dans l'univers.
Nous entamons notre investigation en examinant comment des trames géométriques sont décelables à tous les niveaux de la nature, depuis l'atome jusqu'aux galaxies. Tout d'abord, observons notre environnement proche.
En portant notre attention sur les plantes et les animaux autour de nous, nous découvrons que la nature revêt une grande variété de formes, qui sont généralement arrondies et plutôt irrégulières. Rien ne semble y être géométrique. Pourtant, des structures géométriques sous-tendent en filigrane la plupart des formes naturelles.
Le qualificatif de géométrique nous suggère en premier lieu des carrés, triangles, et autres polygones plus ou moins réguliers, faits de segments droits avec des angles vifs.
C'est bien cet aspect que nous reconnaissons dans les cristaux. Lorsque nous observons des concrétions de calcite ou de quartz, nous constatons qu'elles sont délimitées par des facettes planes régulières. Ces facettes se coupent selon des angles vifs dont les valeurs ne sont pas quelconque, mais déterminées par des symétries. Les facettes planes déterminent des cubes, des prismes, ou d'autres volumes plus complexes à faces planes appelés polyèdres. On trouve aussi de telles géométries régulières cristallines dans de nombreux autres minéraux et dans les cristaux de glace.
Grâce à la découverte des rayons X en 1895 et à celle du phénomène de leur diffraction par les substances cristallines en 1912, les scientifiques ont pu déterminer que les cristaux étaient constitués d'un empilement périodique et régulier de motifs élémentaires composés de quelques atomes. Ce motif appelé maille a la forme d'un polyèdre, cubique, prismatique ou parallélépipédique. On a pu dénombrer 14 modèles différents de polyèdres compatibles avec un empilement régulier (voir l'article détaillé Cristaux et géométrie cristalline).
 |  |  |  |
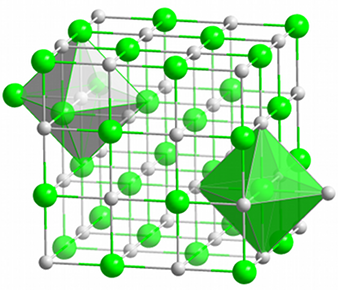| Gerbe de quartz La Gardette, France (Muséum de Genève) Merci à J. Deferne | Réseau cristallin de chlorure de sodium. La structure, soulignée par les barres qui joignent les atomes, est cubique à faces centrées. Les ions sodium (en gris) sont répartis en octaèdres autour de chaque ion chlore (en vert) et vice-versa. Merci à Wikipedia | Carapace de tortue grecque Merci à Calliope | Fleur de nénuphar Nymphaea cruziana © Eric Walravens, Liège |
Même si cela semble moins apparent, on trouve aussi des formes polyédriques chez les animaux et les plantes. Citons les carapaces des tortues ou de crustacés, les cuticules ou les yeux de certains insectes. Quant aux fleurs, nombreuses sont celles qui s'épanouissent en une belle étoile régulière. Les étoiles sont elles-mêmes des polygones dont les angles sont rentrants.
Chez les plantes et les animaux, une observation attentive nous révèle qu'il existe beaucoup de formes géométriques autres que les polyèdres. Les formes en courbes constituent un deuxième type de géométrie abondantes dans la nature. Les spirales en sont les représentantes les plus remarquables. On en a des exemples dans les coquilles d'escargots ou les cornes de bélier.
 |  |  |
| Coquille spiralée d'un escargot Merci à Maths pour les nuls | Fleur de tournesol. Merci à Université de La Réunion, département d'ethnologie | Pomme de pin |
Dans les plantes, leurs éléments (feuilles, fleurs, épines, écailles) s'étagent le long de la tige selon une construction élaborée au cours de la croissance. Cette construction se présente selon deux modes différents. Dans l'un, les éléments sont disposés par groupes de deux l'un en face de l'autre. Dans l'autre, ils naissent l'un après l'autre et se placent en spirales tout autour de la tige.
Dans le cas de la spirale, on constate que les éléments sont placés les uns par rapport aux autres selon un angle dont la valeur est 137,5°. Or cette valeur est celle qui partage la circonférence 360° selon le nombre d'or 1,618. À cause de cette proportion, le nombre de spirales que l'on peut dénombrer dans ces plantes prend des valeurs particulières.
Par exemple, dans une fleur de tournesol, la disposition des fleurons laisse apparaitre de nombreuses spirales. On peut en dénombrer 21 dans un sens et 34 dans l'autre, ou encore 34 et 55, ou 55/89 ou 89/144. Dans un ananas, on peut trouver 8 rangs de fleurons dans un sens et 13 dans l'autre. Dans la pomme de pin, 8 rangs d'écailles dans un sens et 13 dans l'autre ou encore 2 et 3, ou 3/5, 5/8 ou 8/13. Dans la marguerite 21/34 et dans le céleri, 1/2. Or tous ces nombres font exactement partie de la suite étudiée par le mathématicien italien Leonardo Fibonacci (vers 1175 - vers 1250): 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89. Le nombre d'or y transparait dans le rapport de deux de ces nombres consécutifs (voir les détails dans l'article Spirale, mouvement de vie).
Les structures en arborescence, telles que celle d'un arbre, faites de grosses branches qui se ramifient en petites, qui elles-mêmes se ramifient en rameaux, etc. peuvent être décrites comme des structures fractales. C'est un troisième type de géométrie qui ne ressemble ni aux polyèdres ni aux spirales.
Les fractales sont des images de synthèse à 2 ou 3 dimensions comportant des ensembles de points, de lignes, ou de surfaces obtenues par la répétition d'un processus de construction graphique ou mathématique. À chaque étape de répétition est associée une réduction (ou augmentation) d'échelle qui confère aux images obtenues un aspect fragmenté, ramifié ou poreux, qui est identique quelle que soit l'échelle d'observation. Nous découvrirons plus bas les principes de ces procédés graphiques de façon plus descriptive. (voir aussi Images fractales pour plus de détails)
 |  |
| Simulation fractale d'une feuille de fougère Merci à Wikipedia | Simulation fractale d'un paysage montagneux Création © Jean-François Colonna |
Des structures fractales sont sous-jacentes dans des formations naturelles d'apparence irrégulière. On les rencontre dans les réseaux fluviaux, dans la forme déchiquetée des montagnes et dans les formations nuageuses. On en découvre dans la matière fragmentée, découpée, poreuse, filamenteuse. La preuve qu'une structure fractale est sous-jacente à ces formations est qu'il est possible de les simuler graphiquement de façon réaliste par des images fractales de synthèse. C'est par exemple le cas des fougères, des montagnes, des nuages et de beaucoup d'autres matières et paysages.
Nous avons mis en évidence que des géométries, polygones ou polyèdres, spirales et fractales, constituent une armature sous-jacente des formes de la nature.
Afin d'en donner une image plus réaliste, je précise que cette armature n'est pas rigide. Plastique et vivante, la géométrie peut subir des adaptations par rapport à sa forme idéale parfaitement symétrique. On peut se figurer ce caractère en considérant une tente qui prend des aspects bancals si elle est installée sur un terrain irrégulier. Cela ne lui enlève pas sa conception de fabrication avec des armatures parfaitement symétriques et ajustées. Même si elle est installée de travers, sa géométrie parfaite d'origine reste toujours manifeste dans sa forme apparente.
Quittons la Terre et élevons-nous maintenant dans l'espace sidéral. La représentation généralement acceptée est celle d'un univers en expansion depuis la phase initiale du Big Bang. Cela pourrait nous conduire à imaginer que les étoiles sont parsemées au hasard de façon homogène dans le cosmos, comme des cailloux dans un champ. Or ce n'est pas le cas. Allons-nous y trouver des trames géométriques?
Les milliards de milliards de milliards d'étoiles qui peuplent le cosmos ont tendance à s'agglomérer en paquets de dizaines ou de centaines de milliards d'étoiles: les galaxies. Entre les galaxies, subsistent des espaces relativement vides d'étoiles.
La première galaxie découverte fut celle dans laquelle nous sommes situés, la Voie Lactée. À vrai dire, jusqu'au début du 20e siècle, la Voie Lactée semblait s'identifier à la totalité de l'univers. C'est seulement après le développement des télescopes et des spectroscopes qu'on a pu estimer les distances qui séparent la Terre des étoiles visibles. On a pu évaluer approximativement le diamètre de la Voie Lactée.
En astronomie, les distances sont exprimées en années-lumière (al). Une année-lumière est la distance parcourue par la lumière en un an dans l'espace vide, à la vitesse de 300'000 km/s, soit environ 10'000 milliards de kilomètres (300'000x60x60x24x365,25). C'est donc une unité de distance, pas celle d'une durée. Les astronomes emploient également le parsec et ses multiples. Le parsec est une distance liée à un angle d'une seconde d'arc et vaut 3,26 années-lumière.
La Voie Lactée a la forme d'un disque mince renflé en son centre. Son rayon est estimé à 45'000 années-lumière. Le système solaire se trouve vers l'extérieur, à 26'000 années-lumières du centre, soit environ les 2/3 du rayon.
En 1923, Edwin Hubble (astronome étasunien, 1889 - 1953) découvrit que la nébuleuse d'Andromède est située en-dehors de la Voie Lactée, car il estimait son éloignement à 900'000 al. Or elle était reconnue comme étant elle-même une galaxie. C'est le début de la compréhension qu'il existe de nombreuses galaxies en-dehors de la Voie Lactée. À ce jour, le nombre des galaxies cataloguées est démesuré.
Certaines galaxies n'ont aucune forme particulière, mais la plupart adoptent des formes géométriques. Un petit nombre sont elliptiques, d'autres lenticulaires. La majorité des galaxies sont remarquablement spiralées (voir article Spirale, mouvement de vie).
Par la suite, les astronomes se sont aperçus que les galaxies n'étaient pas distribuées de façon homogène dans le cosmos, pas plus que les étoiles en leur sein. Elles sont regroupés en amas.
Ainsi, à côté de la Voie Lactée, on trouve la galaxie Andromède, les nuages de Magellan et une quinzaine de galaxies naines. Cet ensemble est appelé le groupe local. Sa taille est de 13 millions d'al (13 Mal), soit environ 130 fois plus grande que celle de la Voie Lactée.
Les galaxies sont assemblées en groupes, et les groupes sont assemblés en amas qui englobent à la fois des groupes de galaxies et des galaxies isolées. Avec une taille moyenne de 60 Mal, les amas sont environ 5 fois plus grands que les groupes.
Mais ce n'est pas tout. Si nous montons plus haut dans l'échelle des distances, nous nous apercevons que les amas aussi ne sont pas distribués de façon homogène. Les voilà regroupés en super-amas. Un super-amas inclut environ 5 ou 6 amas, et a une taille moyenne d'environ 260 Mal, soit 4 fois plus qu'un amas. Par exemple, le groupe local contenant la Voie Lactée est inclus dans le superamas de la Vierge, également appelé superamas local. Il a été découvert par l'astronome franco-étasunien Gérard de Vaucouleurs en 1960. C'était hier !!
À ce stade de notre exploration, nous avons reconnu 3 niveaux hiérarchiques d'agglomération de galaxies (groupe, amas et superamas). Croyez-vous que cette architecture cosmique s'arrête à cette échelle ? Ce n'est pas le cas, et le plus étonnant est à venir.
En effet, les superamas ont tendance à se rassembler en de vastes filaments longs et minces, ou en feuillets ressemblant à des crêpes. Ces feuillets et ces filaments délimitent de grands espaces vides, comme s'ils étaient placés à la surface de bulles de savon vides. Les bulles de vide cosmique occupent une place prépondérante. Elles ont une taille estimée à 650 Mal, mais certains filaments peuvent être bien plus longs. Quant au vide, il n'est pas réellement vide, mais peuplé de galaxies isolées et d'un gaz ténu.
Avec ces bulles, le cosmos prend l'aspect d'une structure cellulaire. Les cellules (les bulles) sont analogues aux cavités d'une éponge, avec des galeries qui relient les cavités. C'est pourquoi on parle de la structure en éponge de l'univers.
La géométrie cellulaire de l'univers a été découverte dans les années 1990 (Broadhurst, Tully, Einasto). Elle a surpris les astronomes, car aucun modèle issu de la théorie standard du Big Bang ne pouvait l'expliquer.
 |  |
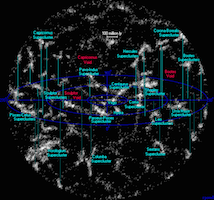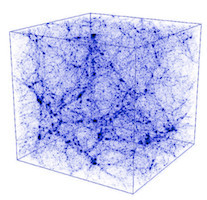| Le super-amas de la Vierge Traduction: cluster = amas; ly=al, années-lumières) Cliquez pour agrandir | L'univers en éponge Cliquez pour agrandir |
Si l'on s'avise de mieux définir la forme des cellules de notre univers proche, on découvre que les bulles ne sont pas rondes. Elles ont la forme particulière de polyèdres. C'est le constat qu'a fait dès 1997 une équipe d'astronomes espagnols incluant E. Battaner et E. Florido. À partir des cartes intégrant les données les plus récentes fournies par les satellites, ces astronomes ont déterminé que les super-amas et les filaments intergalactiques occupaient les sommets et les arêtes de 4 octaèdres qui se touchent par la pointe.
 |  |  |
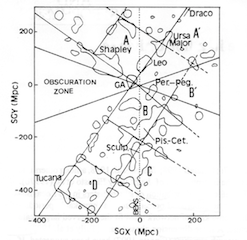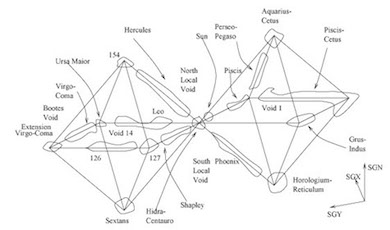| Sur la carte de l'univers proche, on peut identifier au moins 4 octaèdres géants | Les 2 octaèdres les plus proches de la Voie Lactée, les plus faciles à identifier. | Schéma de la structure de l'univers en boite à œufs, faite de l'empilement d'octaèdres se joignant aux sommets. |
| Extraits de Large scale structure and magnetic fields, E. Battaner, © Battaner et Florido | ||
Cette structure n'est pas explicable dans le cadre des modèles habituels basés seulement sur les forces de gravitation. Par contre, si on leur ajoute les champs magnétiques, les calculs montrent que c'est possible. Mais alors, comme ces champs remplissent tout l'espace, ce n'est pas seulement notre univers proche qui aurait cette structure, mais l'univers entier. L'univers aurait l'apparence d'un empilement de cellules octaédriques à la manière d'une boite à œufs.
Parallèlement, à partir des mêmes catalogues de galaxies, d'autres astronomes ont analysé la densité des galaxies, des amas et des super-amas et ils ont découvert que cette densité était distribuée selon une structure fractale. (par exemple Coleman et Pietronero 1992, Lindner et coll. 1996).
On détecte qu'une structure est fractale en mesurant sa densité dans des volumes variant sur de larges échelles. Pour une matière homogène comme de l'eau la masse contenue dans un récipient cubique croit comme la taille du récipient à la puissance 3. Par exemple, si vous remplissez un cube de 10 cm de côté, vous avez un litre. Si vous remplissez un cube de 20 cm de côté, vous avez 8 litres (2x2x2 soit 2 à la puissance 3). Il en est autrement lorsque la structure est fractale. Sa densité croit moins vite que la puissance 3, selon une proportion dont la puissance vaut entre 1 et 3, et qui est appelée sa dimension fractale (voir article Images fractales). La dimension fractale de l'univers a été évaluée à 2 par Coleman.
Battaner (1998) considère que ce caractère fractal est tout à fait compatible avec la structure des cellules en octaèdres. Il suffit de fragmenter chaque octaèdre en octaèdres plus petits. Par exemple, dans un octaèdre, peuvent se loger 7 octaèdres 3 fois plus petits qui se touchent uniquement par la pointe.
Sources: Les différents types de galaxies, Olivier Esslinger, site web astronomes.com; Les galaxies, site web nrumiano.free.fr; Large scale distribution of galaxies at the galactic poles, Broadhurst Thomas J. et al. 1990, Nature 343, 726-728; The fractal structure of the universe, Paul H. Coleman, Luciano Pietronero, 1992, Physics Reports, 213, 6, 311-389; The structure of supervoids. I. Void hierarchy in the Northern Local Supervoid, Lindner U., Einasto J., Einasto M., Freudling W., Fricke K., Tago E., 1995, Astronomy and Astrophysics, v.301, p.329; The Distribution of galaxies in Voids, Lindner U., Einasto M., Einasto J., Freudling W., Fricke K., Lipovetsky V., Pustilnik S., Izotov Y., Richter G., 1996, Astronomy and Astrophysics, 314, 1 - 12; A 120 mps scale in the universe, J. Einasto, 1997, Talk on conference "The Birth of the Universe II" ed. F. Occhionero; Kluwer Sci. Publ.; Magnetic fields and large scale structure in a hot Universe. IV. The egg-carton Universe, E. Battaner and E. Florido, Astron. Astrophys., 1998, 338, 383-385, également en pdf ICI; The fractal octahedron network of the large scale structure, E. Battaner, 1998
Depuis l'infiniment grand transportons-nous dans l'infiniment petit. Ce monde, très éloigné de notre expérience quotidienne, se montre complexe et étrange. Nous allons découvrir que les atomes sont structurés par des géométries.
La géométrie des atomes ne se laisse pas appréhender par l'observation, car ils sont trop petits pour que nous puissions les observer, même avec de puissants microscopes. C'est par la façon dont ils réagissent aux rayonnements qu'on peut se rendre compte de leur structure interne.
En exposant les atomes à un rayonnement X, le physicien néo-zélandais Ernest Rutherford s'est aperçu que la répartition des rayonnements réfléchis et diffusés pouvait se comprendre si on représente l'atome comme composé d'un noyau concentré au centre, et d'un cortège d'électrons qui circulent autour (voir article Matière et rayonnements). Les électrons portent une charge électrique négative. Grâce à d'autres mesures effectuées par la suite, on a précisé que le noyau est constitué de particules nommées nucléons qui sont de deux types, les protons et les neutrons. Les neutrons n'ont pas de charge électrique. Les protons ont une charge positive. Leur nombre est égal au nombre des électrons, de sorte que les charges électriques de l'atome s'équilibrent.
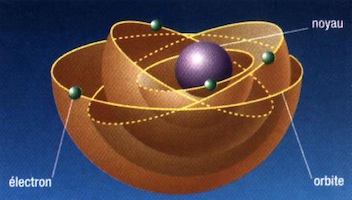
Il ne faut pas perdre de vue que cette description n'est qu'un modèle commode qui permet de rendre compte des observations expérimentales. Ce modèle peut tout aussi bien être remplacé par un autre si de nouvelles expériences s'avéraient ne pas être en accord avec lui. Pendant un temps, le physicien danois Niels Bohr avait proposé que les électrons décrivent des orbites autour du noyau, à la façon des planètes autour du soleil. Mais il a rapidement abandonné ce modèle qui n'est plus admis par les physiciens aujourd'hui.
Le modèle admis repose sur les principes de la physique quantique, qui énonce que les électrons sont impossibles à localiser. On ne peut donc pas parler d'orbite. On ne peut qu'indiquer la probabilité de leur présence dans un endroit donné. La région où leur présence est la plus probable constitue une orbitale (voir article Physique quantique).
Que l'on parle d'orbite ou d'orbitales, les expériences indiquent qu'elles ont une symétrie sphérique. Ainsi, les orbitales ressemblent à des coques sphériques aux limites floues qui entourent le noyau. Lorsque deux ou plusieurs atomes sont associés, leurs orbitales se combinent en sphères doubles, triples, quadruples, ou encore des ellipsoïdes ou autres surfaces de révolution, composant des sortes de fleurs.
Un autre type de géométrie présente dans les atomes résulte de la structure en couches et sous-couches de ces orbitales. Les nombres maximum d'électrons dans les 4 sous-couches sont 2, 6, 10 et 14, qui s'additionnent en couches de 2, de 8, de 18 et de 32. Cette constatation a été déduite par les chimistes de l'étude des propriétés des éléments chimiques. Ils ont constaté que des propriétés semblables revenaient de façon cyclique en fonction de la masse de leur atome constitutif. La masse des atomes est directement liée au nombre de nucléons. Si la masse augmente, le nombre de nucléons est plus grand, et il en est de même du nombre d'électrons. Au fur et à mesure que le nombre d'électrons croît, ils remplissent progressivement les couches et sous-couches orbitales des atomes. (voir plus de détails en annexe)
Au remplissage des orbites par des électrons correspond l'augmentation du nombre des protons dans le noyau. De certaines considérations sur les propriétés des noyaux, la physicienne étasunienne, Maria Goeppert Mayer (née en Allemagne en 1906 - 1972, prix Nobel de physique en 1963) a déduit un modèle de la répartition en couches des nucléons. La contenance en nucléons de chacune des 8 couches est: 2, 8, 20, 28, 50, 82, 126 et 184. (voir plus de détails en annexe)
En 1986, le Pr Robert J. Moon (physicien et chimiste étasunien, 1911 - 1989) proposa un autre type de modèle nucléaire. Il tient compte seulement des protons, laissant de côté les neutrons, donc les isotopes.
Moon est frappé par les résultats des mesures de conductivité électrique faites en 1980 par le physicien allemand Klaus von Klitzing (né en 1943). Dans ses expériences, Klitzing prend un ruban de divers matériaux conducteurs, les refroidit à basse température et les met sous l'influence d'un champ magnétique. Il constate que leur conductivité ne varie pas de façon continue avec la température, mais par des sauts (phénomène nommé effet Hall quantique). La conductivité est quantifiée.
Pour le Pr Moon, les phénomènes de quantification sont la manifestation des propriétés de l'espace, pas seulement celles du matériau. Or les polyèdres de Platon représentent des symétries particulières de l'espace, et selon Moon, ils doivent être introduits dans son modèle.
| Les 5 polyèdres de Platon Merci à Robert Ferréol et Alain Esculier | ||||
|---|---|---|---|---|
 |  |  |  |  |
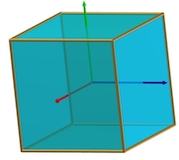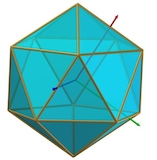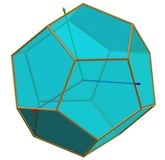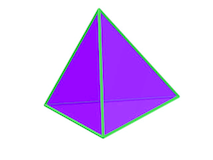| Cube 6 carrés 8 sommets | Octaèdre 8 triangles 6 sommets | Icosaèdre 20 triangles 12 sommets | Dodécaèdre 12 pentagones 20 sommets | Tétraèdre 4 triangles 4 sommets |
Robert J. Moon, docteur en physique et chimie physique, fut dans les années 1930/40 un pionnier en physique des particules et de l'énergie nucléaire. Il construisit le deuxième cyclotron au monde, introduisant de nombreuses améliorations par rapport à celui de E.O. Lawrence. Il a joué un rôle important dans le projet Manhattan pendant la deuxième guerre mondiale, en résolvant le problème de la modération de la fission nucléaire par le graphite. Après la guerre, il construisit le premier microscope à balayage de rayons X, et mena des recherches d'avant-garde dans le domaine de la biophysique.
Son approche du noyau atomique s'écarte des considérations de ses contemporains, qui sont liés exclusivement aux expériences de diffraction de Rutherford. Moon remarque que les calculs de Rutherford, qui font encore foi de nos jours, ne tiennent pas compte de l'accélération des particules chargées. Moon se sert de certains aspects négligés des théories électrodynamiques de André-Marie Ampère et de Wilhelm Weber.
Wilhelm Eduard Weber (physicien allemand, 1804 - 1891) a démontré que deux particules de même charge électrique, par exemple deux protons du noyau, qui normalement se repoussent, peuvent aussi s'attirer lorsqu'elles sont suffisamment proches, en-dessous d'une distance maximale. Une telle association de deux particules, appelée paire de Weber, est stable dans un mouvement d'oscillation le long de la ligne droite qui les relie. Pour les protons, la distance maximale est de 3x10-16 cm. Il est donc inutile d'inventer l'existence d'une force nucléaire pour justifier la stabilité d'un assemblage de protons.
Laurence Hecht (directeur de 21th century science and technology magazine) a étendu les travaux de Moon en incorporant les neutrons dans le modèle nucléaire. Pour lui, comme pour Moon, le principe d'indétermination et l'introduction excessive du hasard dans les approches de Niels Bohr, Wolfgang Pauli et Werner Heisenberg ont eu pour conséquences dévastatrices le rejet du principe de causalité en physique et l'abandon de la recherche de principes d'ordonnancement de l'univers. Moon, Hecht et Stevens sont revenus à de tels principes en s'inspirant de l'électrodynamique de Gauss, Ampère et Weber.
Les polyèdres sont des volumes, tels que le cube ou le tétraèdre, qui sont délimités par des faces planes. Les polyèdres de Platon sont des polyèdres réguliers convexes qui peuvent s'inscrire dans une sphère. Convexe signifie qu'ils n'ont pas de creux, contrairement à un polyèdre étoilé. Tous les côtés et tous les angles d'un polyèdre régulier sont égaux. On dénombre 5 polyèdres de ce type.
Dans son modèle, Moon utilise quatre des cinq polyèdres de Platon, assemblés par emboitement les uns dans les autres. Les protons sont placés successivement aux sommets de chacun des polyèdres de cette structure.
Au centre se tient le cube. Il comporte 8 sommets. Le remplissage en protons correspond aux éléments depuis l'hydrogène (Z=1) jusqu'à l'oxygène (Z=8).
Autour du cube vient s'imbriquer un octaèdre avec 6 sommets. Cela génère les éléments depuis le fluor (Z=9) jusqu'au silicium (Z=14). Ensuite vient se placer l'icosaèdre avec 12 sommets supplémentaires, du phosphore (Z=15) au fer (Z=26). Enfin le tout est entouré d'un dodécaèdre, avec 20 sommets, du cobalt (Z=27) au palladium (Z=46). Au-delà, il faut accoler sur une face commune une deuxième structure semblable, ce qui nous conduit à l'uranium (Z=92).
 |  |
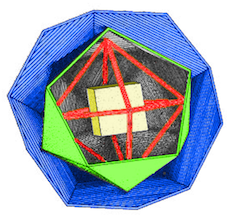| Le Pr. Robert J. Moon vers 1986 | Structure géométrique du noyau atomique de Robert Moon Du centre vers la périphérie: le cube (jaune), l'octaèdre (rouge), l'icosaèdre (vert) et le dodécaèdre (bleu). © A. Boudet, d'après un dessin original de Nouvelles avancées, par Laurence Hecht, revue Fusion, 1987 |
Les périodicités qui se révèlent dans le modèle de Moon sont 8 (oxygène), 6 qui, par addition donne 14 (8+6, le silicium), 12, qui donne 26 (8+6+12 - fer), et 20 qui donne 46 (8+6+12+20 - palladium).
Si nous nous reportons à la courbe des volumes atomiques classés par numéro atomique croissant (voir en annexe), on constate que ces éléments se trouvent aux minimums ou quasi-minimums des volumes atomiques. Cela suggère qu'ils correspondent à une compactification maximum, lorsqu'un polyèdre est complètement plein. De même en ce qui concerne les susceptibilités magnétiques, on peut noter que l'oxygène, le fer et le palladium se trouvent aux maximums de la courbe.
Sources: Le tableau périodique et Mendeleïev, site web la chimie.net; Tableau périodique des éléments, site wikipédia; Tableau périodique des éléments dans le site web tableau-periodique.fr; Tableau périodique des éléments dynamique, par Michael Dayah; Who was Robert J. Moon?, 21st century science and technology magazine; The geometric basis for the périodicity of the elements, Laurence Hecht, 21th century, may-june 1988; Robert J. Moon: On how he conceived his nuclear model, 1987 presentation, 21th century magazine, fall 2004; Modèle géométrique du noyau atomique: nouvelles avancées, Laurence Hecht, revue Fusion n°84, janvier 2001
Entre l'infiniment grand et l'infiniment petit, revenons à notre planète Terre, en l'envisageant dans sa globalité sphérique. En elle-même, la forme sphérique de la Terre, bien visible depuis l'espace, constitue à l'évidence une géométrie. Son axe de rotation en est un élément supplémentaire essentiel. Mais c'est une autre géométrie que nous allons aborder. Nous allons découvrir que la Terre est architecturée par une trame géométrique, qui n'est visible que par un examen attentif. Et nous y retrouverons les polyèdres de Platon !!
Puisque les polyèdres sont définis par des lignes droites, nous pouvons nous attendre à déceler ces lignes à la surface de la terre. En effet, elles sont mises en évidence par des alignements ponctués par des sites sacrés. L'un des pionniers de l'étude des alignements de sites sacrés a été l'anglais Alfred Watkins vers 1920. Dans la campagne du Sud de l'Angleterre, il observa que des sites sont fréquemment alignés sur des kilomètres. Il nomma ces lignes lignes de ley. Les sites ainsi pris en compte sont des pierres levées (menhirs), des collines rondes artificielles, des tumulus, des sources sacrées ou encore des églises. D'autres chercheurs se rendirent compte que de telles lignes existaient aussi en Europe et en Amérique. En se recoupant, elles déterminent des triangles, des hexagones et d'autres polygones, dont le réseau couvre la planète entière en une sorte de grille (voir article Alignements de lieux sacrés).
Ces lignes fonctionnent à la manière de canaux ou de vaisseaux qui conduisent l'énergie vitale de la planète, de la même manière que le corps humain est irrigué par d'innombrables vaisseaux, les nadis et méridiens d'acuponcture décrits par les textes védiques (voir article Chakras et corps subtils). La grille constitue une armature qui alimente la planète en flux vitaux indispensables à sa propre vie et à celle de ses habitants de tous les règnes (plantes, animaux, humains, minéraux).
La majorité des constructions sacrées sont implantées soit sur ces lignes, soit sur leurs croisements (les sommets des polygones), à cause de l'énergie vibratoire spéciale qui émane de ces lieux. Les monuments sacrés ont plusieurs fonctions. Ils collectent et régulent l'énergie qui s'y manifeste. À cause de ces énergies spéciales, les nœuds ou croisements de la grille sont fréquemment le siège d'anomalies magnétiques ou géophysiques, ou encore de manifestations climatiques particulières. Certains d'entre eux ont acquis une réputation sinistre comme le triangle des Bermudes ou le triangle du diable au large du Japon.
Vers 1970, en repérant les emplacements de ces anomalies, trois scientifiques russes, Nikolai Goncharov, Valery Makarov et Vyacheslav Morozov, mirent en évidence l'existence d'un réseau planétaire principal, qui est architecturé par des polyèdres. Par la suite, vers 1983, ce réseau fut complété et ajusté par un couple étasunien, le Dr William Becker et son épouse le Dr Bethe Hagens.
 |  |  |
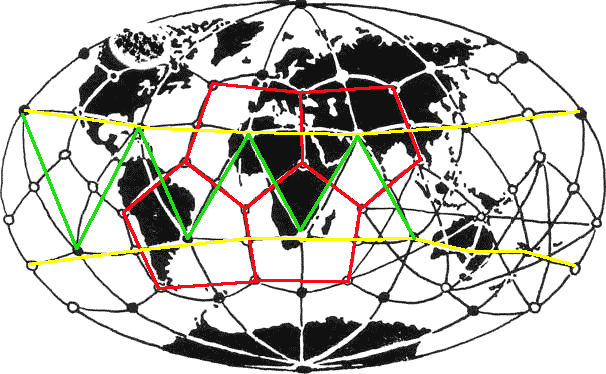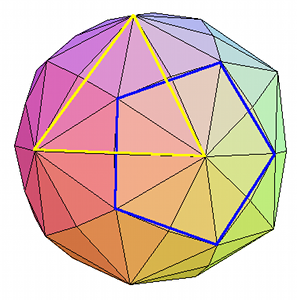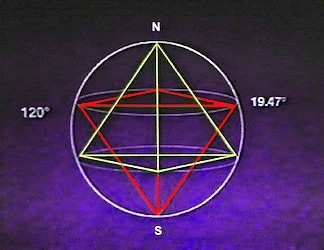| La grille planétaire de Goncharov, Makarov et Morozov En vert, l'icosaèdre, en rouge le dodécaèdre | Le polyèdre à 120 triangles de la grille planétaire de Becker-Hagens | Double tétraèdre inscrit dans une sphère. Merci à R. Hoagland |
La grille énergétique planétaire de Becker-Hagens est composée de 120 triangles. Les 5 polyèdres de Platon sont inscrits dans cette grille, principalement l'icosaèdre et le dodécaèdre. Les 3 autres (octaèdre, tétraèdre et cube), plus discrets, y sont également présents.
Examinons par exemple où se loge le tétraèdre. À cause de l'axe de rotation de la Terre, l'un de ses sommets du tétraèdre est positionné sur l'un des pôles. Cela entraine que les trois autres sommets sont répartis sur le parallèle de longitude 19°28' (soit 19,47° en coordonnées décimales). Il existe donc deux tétraèdres possibles, l'un ancré au pôle sud, l'autre au pôle nord. Les 3 sommets du tétraèdre de pôle nord, de longitude 19,47° Sud, sont situés dans l'océan. En ce qui concerne le tétraèdre de pôle sud, ses sommets sont situés à la longitude 19,47° Nord. Selon Carl Munck (The Code, 1997), l'un des sommets est représenté par une bande verticale étroite de largeur 1° qui couvre le Nil et toutes ses pyramides, en particulier la Grande Pyramide. Le deuxième sommet est représenté par une deuxième bande verticale qui traverse le Yucatan au Mexique et au Guatemala, où sont construites de nombreuses pyramides mayas, comme la pyramide de Tikal au Guatemala.
Munck ne parle pas du troisième sommet, mais j'ai pu facilement calculer qu'il coïncide avec une bande verticale épousant l'arc volcanique des iles Mariannes et la grande fosse océanique des Mariannes. (Pour plus de détails, voir article Réseaux planétaires et polyèdres)
Les polyèdres qui sous-tendent la planète se manifestent parfois en guidant les mouvements de la croûte terrestre. C'est le cas des déplacements des plaques tectoniques. De quoi s'agit-il?
Lorsque nous observons une carte géographique des continents, nous sommes frappés par la similitude des profils de la côte Est de l'Amérique du Sud et de la côte Ouest de l'Afrique. Si nous pouvions rapprocher ces côtes, il semble qu'elles pourraient s'emboiter parfaitement l'une dans l'autre. C'est ce qu'avait remarqué plusieurs savants dès le 19e siècle. En partant de cette observation, l'allemand Alfred Wegener proposa sa théorie de la dérive des continents en 1912. Il avança que les continents se déplacent très lentement à la surface de la Terre et bougent les uns par rapport aux autres. Ainsi, les côtes africaines et américaines auraient par le passé été assemblées et se seraient séparées ensuite en s'écartant de plus en plus. En remontant le film à l'envers dans le temps, Wegener imagina que tous les continents étaient autrefois réunis en un seul grand supercontinent, la Pangée (Pangaea : Terre totale en grec). Puis la Pangée se serait progressivement disloquée il y a 250 millions d'années. Ses morceaux ont dérivé et se sont fragmentés jusqu'à donner les continents actuels. Plus tard, des scientifiques ont conforté la thèse des continents autrefois réunis en relevant des similitudes entre la faune et la flore de continents éloignés, qui pourraient s'expliquer par les passages qui les auraient reliés par le passé.
Cette théorie n'obtint pas les faveurs de la communauté scientifique. Il fallut attendre les années 1960 où elle fut renforcée par la théorie de la tectonique des plaques élaborée par Dan McKenzie, William Morgan, Xavier Le Pichon, Robert Parker et John Wilson. Selon cette théorie, les continents sont portés par des plaques de la croute terrestre. Les plaques flottent sur le magma liquide et dérivent les unes par rapport aux autres. Elles s'éloignent, ou se rapprochent et s'entrechoquent, ou encore se frottent l'une contre l'autre. Leur vitesse relative est de quelques centimètres par an. En s'éloignant, elles laissent entre elles un espace qui se remplit d'une nouvelle matière qui surgit des fonds marins et forme des crêtes océaniques. Un exemple de crête est celle du milieu de l'océan atlantique.
Les bordures des plaques tectoniques sont repérées par les crêtes, les fosses océaniques et les rangées de volcans et d'arcs insulaires. On a dénombré une douzaine de plaques. Mais délimiter des plaques n'est pas si évident et leur nombre est approximatif.
 |  |
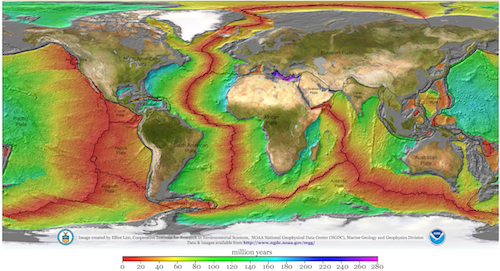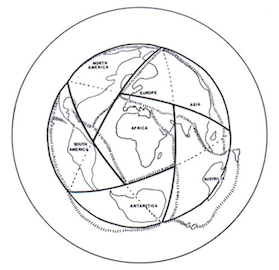| Carte des plaques du plancher océanique Cliquez pour agrandir l'image Merci à NOAA Marine Geology and Geophysics Source: Age, spreading rates and spreading symmetry of the world ocean crust, Muller R.D., Sdrolias M., Gaina C., Roest W.R., Geochem. Geophys. Geosyst. 9, Q04006, 2008 | Les limites principales des plaques tectoniques (lignes pointillées) comparées à un icosaèdre (lignes continues) Extrait de: A. Spilhaus, Geo-art: plate tectonics and Platonic solids, American Geophysical Union Transactions, vol. 56, 1975, pp. 52-57. Cité par D. Pratt |
Le point d'intersection de deux bordures est un point de jonction de trois plaques. On peut repérer plusieurs de ces points triples sur la carte des plaques. En 1976, le Dr Athelstan Spilhaus (géophysicien et océanographe d'Afrique du Sud, naturalisé étasunien, consultant de National Oceanographic and Atmospheric Administration ou NOAA, 1911 - 1998) examina ces points triples, en s'appuyant sur les résultats des recherches de Hanshou Liu au Goddard Space Flight Center, important centre de recherches de la NASA aux États-Unis. En les reportant sur un globe, il remarqua que les points triples coïncident presque parfaitement avec les sommets d'un icosaèdre.
Le Dr Spilhaus affirme que l'icosaèdre serait la dernière phase de l'évolution terrestre. En effet, la Pangée, au cours de sa dislocation, serait passée par trois phases. Elle aurait d'abord épousé la trame d'un tétraèdre, puis celle d'un cuboctaèdre (un cube tronqué à ses sommets), et enfin celle actuelle de l'icosaèdre associé au dodécaèdre.
Si les plaques avaient dérivé de façon chaotique, cette succession de géométries régulières serait bien surprenante. Mais si on admet que la Terre est structurée par une armature constituée des polyèdres de Platon, on peut comprendre que cette armature est le siège de concentrations de forces qui peuvent induire les fissurations ou guider les déplacements des masses.
La théorie de la tectonique des plaques a changé notre façon de voir la Terre. La planète est devenue un corps qui se transforme en permanence. Toutefois, la théorie comporte des lacunes et de nombreuses incohérences. Même s'il faut en garder l'aspect de transformation des masses terrestres, nous devons examiner d'autres théories qui rendent compte des mesures actuelles de façon plus exacte.
Initialement, les données sur la dérive des terres étaient trop grossières pour qu'on se rende compte de leur incompatibilité avec la théorie. Depuis ce temps et jusqu'à aujourd'hui, des mesures abondantes et bien plus précises ont été effectuées, à la fois par tomographie sismique, repérage par satellites, et forage de fonds marins. Il s'est avéré que les valeurs recueillies sont loin d'être homogènes et ne sont pas en accord avec le modèle de grands blocs qui dérivent sur une couche liquide. Les déplacements s'avèrent localisés, variant d'un endroit à l'autre.
Les valeurs ne sont pas plus en accord avec le modèle d'écoulement global du manteau et des zones de subduction marines. De même que dans de l'eau en ébullition dans une casserole, apparaissent des rouleaux de courants formant de petites cellules (voir rouleaux de Bénart dans l'article Sons créateurs de formes), de même le magma est le siège de mouvements cellulaires de convection. Les mesures sont cohérentes seulement avec des cellules de petite taille.
Par ailleurs les mouvements verticaux ne sont pas pris en compte dans la théorie de la tectonique des plaques. Or de nombreuses observations de couches de sédiments dans des zones continentales montrent qu'elles ont autrefois été submergées et ont subi des mouvements verticaux d'affaissement et d'élévation. Inversement, il y a de fortes présomptions que des blocs de la croute terrestre actuellement submergés ne l'étaient pas dans le passé.
La tectonique verticale est une théorie alternative qui prend en compte à la fois des montées verticales du magma et des déplacements locaux de surface. Dans cette théorie, les cellules de magma communiquent et sont disposées en un réseau qui couvre la planète entière. Il est intéressant de noter que les auteurs de cette théorie ont qualifié ce réseau de réseau cardiovasculaire de la Terre !.
Une autre théorie alternative révolutionnaire prétend que la Terre a progressivement augmenté de volume au cours des âges à partir de l'ère jurassique. À cette époque, son rayon était réduit de 40 ou 50% par rapport au rayon actuel. Sur la Terre ainsi réduite en volume, la Pangée couvrait parfaitement la surface entière de la Terre. Ensuite, au fur et à mesure que le rayon augmentait, les plaques tectoniques rigides se sont craquelées puis se sont écartées, de façon analogue à des morceaux de terre séchée appliqués sur un ballon que l'on gonfle. En s'élargissant, les craquelures se sont remplies d'eau et ont formé les océans.
Cette théorie a été élaborée progressivement par une lignée de chercheurs. Elle a commencé avec le travail d'avant-garde de Ott Christoph Hilgenberg en 1933 (chercheur et ingénieur allemand, 1896 - 1976). Le géologue australien Samuel Warren Carey (1911 - 2002) y a apporté une contribution essentielle. Elle a été enrichie des travaux d'autres auteurs, essentiellement allemands et russes. Actuellement, elle est activement défendue par plusieurs chercheurs, dont l'allemand Klaus Vogel et le géologue australien James Maxlow (né en Angleterre en 1949, émigré en Australie). À l'appui de cette théorie qu'il a nommée la tectonique d'expansion globale, Maxlow constate que les mesures récentes de déplacement de surface locaux, effectuées à partir de satellites, sont compatibles avec une augmentation du rayon terrestre d'environ 2 cm par an.
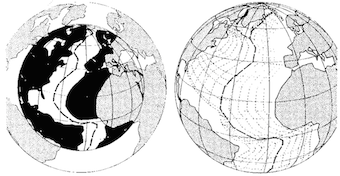
À gauche, schéma de la Terre dans une phase initiale contractée (continents représentés en noir). À droite, la position actuelle des continents après dilatation.
Reconstruction par ordinateur par Perry. Extrait de Carey S.W., Diapiric krikogenesis, 1986, dans International Conference on "The Origin of Arcs", Urbino, Italy, September 1986, pp 1-40, ed. G. Scalera. Cité par J.
Maxlow
Pour souligner l'importance et le sérieux de la théorie d'expansion globale de la Terre, alors qu'on en parle très peu, je cite l'essentiel des chercheurs qui y ont contribué et contribuent encore: Vogel (travaux publiés en 1933, puis 1983, 1984, 1990), Halm (1935), Keindl (1940), Egyed (1956), Carey (1958), Heezen (1959), Brösske (1962), Barnett (1962, 1969), Dearnley (1965), Creer (1965), Shields (1976, 1979, 1983, 1990), Owen (1976, 1983), Schmidt and Embleton (1981), Neiman (1984, 1990). Vogel déjà cité, Perry (1986) et Scalera (1988) ont produit des modèles élaborés.
Pour Klaus Vogel, les mesures relevées sur les fonds océaniques montrent que globalement, les continents tendent à se déplacer radialement par rapport à leur position au précambrien jusqu'à leur position moderne et que c'est considéré comme une étrange coïncidence pour toutes les théories, sauf celle de l'expansion de la Terre. Le géophysicien italien Giancarlo Scalera a écrit: L'histoire de la Terre, inscrite et clairement lisible au fond des océans, n'est pas l'histoire de la tectonique des plaques mais l'histoire d'une planète en expansion.
Si, à ce modèle, nous associons les conclusions de Spilhaus de la section précédente, la structuration polyédrique des plaques qu'il a mise en évidence se révèle encore plus significative. Nous comprenons en effet qu'au cours de la dilatation de la Terre, les plaques sont guidées dans leur mouvement par l'armature énergétique polyédrique de la Terre.Sources: Sunken Continents versus Continental Drift, David Pratt, Dec 2000, last revised Mar 2011; Global expansion tectonics, Exponential Earth Expansion from the Pre-Jurassic to the Present, James Maxlow; Expansion terrestre, wikipedia
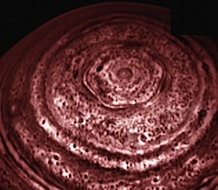
La Terre n'est pas la seule planète à contenir des structures géométriques. Les planètes du système solaire en sont aussi dotées.
Dans le système nuageux de Saturne, la sonde Voyager 1 a détecté en 1980 une structure hexagonale autour du pôle nord. Son existence a été confirmée par la sonde Cassini en 2006. Les côtés de l'hexagone mesurent environ 13'800 km. Il tourne sur lui-même avec une période de 10h 39 min.
Le pôle nord de Jupiter a été photographié en lumière ultraviolette par la sonde Cassini pendant 11 semaines en 1999. On y remarque la présence d'un tourbillon en forme de pentagone.
Tout comme dans la Terre, il est possible de définir une architecture en forme de tétraèdre qui sous-tend la plupart des planètes. C'est ce qu'a énoncé David Percy, un producteur de cinéma et de télévision britannique qui a aussi reçu la fonction de directeur européen des opérations pour la mission Mars. Ses propositions, présentées dans son ouvrage Two-thirds (Deux-tiers, en collaboration avec David P. Myers et Mary Bennett), ont été reformulées et popularisées par Richard Hoagland, un ancien conseiller de la NASA pour le Goddard Space Flight Center.
Nous avons vu plus haut, à propos de la Terre, que les sommets d'un tétraèdre sont localisés à la latitude de 19,47°. Percy et Hoagland ont mis en évidence des phénomènes importants situés à la latitude de 19,47° Nord ou Sud dans le système nuageux de plusieurs planètes. La grande tache rouge de Jupiter est située à cette latitude. Il en est de même de la tache noire de Neptune découverte par la sonde Voyager II. Les activités volcaniques majeures de Vénus se situent autour de 19,5°. Le Mont Olympe, cône volcanique de Mars est à cette même latitude. Enfin, les fortes activités magmatiques et thermiques du Soleil se produisent à 19,5° Nord et Sud. (plus de détails dans l'article Sons créateurs de formes)
Aventurons-nous maintenant dans le corps humain. Pouvons-nous y déceler des trames géométriques? À l'intérieur, nous découvrons une complexité géométrique impressionnante.
En premier lieu, nous rencontrons à nouveau la spirale. Puisqu'elle est présente dans les plantes et les animaux, il aurait été étonnant que nous ne l'y trouvions pas chez l'homme. Exprimant le mouvement de vie primordial, elle se loge dans l'arrangement torsadé des fibres du cœur et des artères qui impriment au flux sanguin un mouvement hélicoïdal. Nous la trouvons aussi dans la cochlée, la partie sensible aux sons de l'oreille interne. Au niveau moléculaire, elle se manifeste dans les conformations des protéines et la structure en double hélice de l'ADN (voir détails dans l'article Spirales, mouvements de vie).
En second lieu, l'organisation hiérarchique, collective et rétroactive (en science on dirait systémique) des différents systèmes anatomiques du corps force l'admiration. Les organes participent au bon fonctionnement du corps, de façon précise, avec une adaptation constante. Ils sont capables de se réparer eux-mêmes en cas de lésion. Les organes et les tissus sont organisés en systèmes (respiratoire, nerveux, sanguin, digestif, etc) capables de transformer les impressions et sollicitations extérieures, et de réagir par des réponses intelligentes. Les cellules se développent et se différencient en organes au bon endroit et au bon moment. Tout cela fonctionne en parfaite harmonie dans une gamme de circonstances extérieures très étendue et très variable, allant quelquefois jusqu'à des conditions extrêmes.
Si nous examinons la silhouette du corps, nous distinguons différentes parties articulées les unes par rapport aux autres. Tête, tronc, bras et jambes s'assemblent en une structure géométrique. Un enfant ne s'y trompe pas puisqu'il représente ses personnages par un assemblage de ronds et de segments.
La vision d'un corps humain structuré par des géométries est parfaitement familière aux artistes. Certains peintres, certains sculpteurs, certains fabricants de poupées ou de figurines pour jouets d'enfants, donnent de leurs personnages des représentations très stylisées, réduites parfois à quelques volumes tout à fait caractéristiques, carrés, trapèzes, cercles, ovales, ou à une sorte de squelette fait de segments de droite articulés. Malgré cette simplification exagérée, le personnage est bien reconnaissable. Ceci prouve que l'essentiel du corps a été perçu et représenté. Et que cet essentiel est fait de géométrie.
 |  |  |
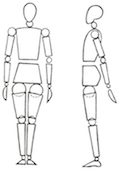| Dessin d'un enfant de 6 ans Merci à Bérangère | Figurine Lego ancienne Cette expression tranquille des anciennes figurines a été remplacée par des expressions agressives de colère et de méchanceté. Surprenant ! | Trame géométrique du corps humain, servant de lignes de construction pour un dessin |
De même, lorsque des dessinateurs veulent dessiner un corps humain, ils esquissent d'abord ses volumes généraux au moyen de lignes de construction adoptant la forme de trapèzes, de carrés ou de cercles, qu'ils habillent ensuite de chair pour leur donner leur apparence réelle.
Ces volumes doivent respecter certaines règles de proportion entre eux, si l'on veut faire ressortir un certain type de beauté des personnages (des beautés qui ne sont pas forcément standardisées sur un seul modèle, elles peuvent afficher une certaine diversité !). Certaines de ces règles ont été proposées par le peintre Léonard de Vinci (également ingénieur, anatomiste, sculpteur...). Dans son célèbre dessin intitulé Étude des proportions du corps humain selon Vitruve (1492), il a actualisé et mis en image les conceptions de l'architecte romain Vitruve (90 av. J.C. environ - 20 av. J.C. environ) exposées dans son ouvrage De l'architecture. Dans le dessin de Vinci, on remarque que le corps humain est inscrit dans un cercle dont le centre est le nombril, et dans un carré dont le centre est le pubis.
 |  |
| Étude des proportions du corps humain selon Vitruve Léonard de Vinci, Plume, encre et lavis sur papier vers 1490 Merci à Wikipédia | L'Adam Kadmon en lien avec Dieu et l'univers. Miniature de Hildegarde de Bingen, dans Liber divinorum operum Codex latinus, vers 1230, Lucques, Bibliothèque d'Etat (vision 2, fol. 6) Merci à Images re-vues |
Au 12e siècle, bien avant De Vinci, l’abbesse bénédictine rhénane Hildegarde von Bingen (1098-1179) a formulé des indications sur les proportions du corps humain. Elle recevait ses connaissances sous la forme d'images accompagnées de commentaires auditifs, destinées à aider les êtres humains à se réaliser en Christ. C'est ainsi qu'elle a acquis des compétences multidisciplinaires, en médecine, et en musique aussi bien que comme prophétesse. Certains passages de ses ouvrages décrivent la relation de l'homme accompli, l'Adam Kadmon, avec le cosmos dans ses aspects aussi bien astronomique que divin. Les miniatures qui les illustrent représentent l'homme dans une imbrication de cercles et de rectangles.
Dans le Livre des Œuvres divines, elle écrit: Dans la rotondité de la tête humaine, c’est la rotondité du firmament que l’on retrouve. Les dimensions justes et rigoureuses du firmament correspondent aux mêmes dimensions de la tête de l’homme. Celle-ci a donc ses mesures exactes, comme le firmament, qui répond lui aussi à des mesures rigoureuses, afin de pouvoir accomplir une révolution parfaite, afin qu’aucune partie n’outrepasse injustement la mesure d’une autre. C’est que Dieu a façonné l’homme sur le modèle du firmament et il a conforté son énergie par des forces élémentaires.
Récapitulons: L'univers entier, à tous les niveaux de la création, est tissé par des structures géométriques abstraites. Même le corps humain est sous-tendu par des géométries faites de polyèdres et de spirales.
Or les géométries sont intimement liées à des sons.
Les vibrations sonores ont le pouvoir de modeler la matière fluide ou plastique pour créer des géométries. Cela a été montré dès le 18e siècle par le physicien allemand, Ernst Chladni (prononcez kladni). Après avoir abondamment saupoudré de sable une plaque de verre ou de cuivre, Chladni en frotte le bord avec un archet de violon. La plaque se met à vibrer et produit un son. Sous l'effet des vibrations, les grains de sable se déplacent et se rassemblent dans les endroits les plus calmes de la plaque et forment un ensemble de lignes.
Pour certaines fréquences sonores précises, les lignes dessinent des figures géométriques spectaculaires. En faisant varier la force de frottement de l'archet, sa vitesse et son point d'application, Chladni obtint des figures très variées.
 |  |  |
| Figure de sable sur une plaque ovale soumise à un son de fréquence 2515 Hz Photos © A. Lauterwasser, Images sonores d'eau | Figures obtenues dans un film d'eau, sous l'influence de fréquences sonores | |
| Polygone à 5 branches. Fréquence 38,45 Hz © A. Lauterwasser, Images sonores d'eau | Spirale à 14 bras. Fréquence 102,528 Hz. © A. Lauterwasser, Images sonores d'eau | |
Par la suite, d'autres expérimentateurs ont exploré comment le son façonne des matières diverses, à la condition qu'elles soient suffisamment malléables. En Suisse, Hans Jenny (1904 -1972) a observé les figures obtenues avec des poudres, des liquides et des pâtes. Plus récemment, en Allemagne, l'expérimentateur, philosophe et photographe Alexander Lauterwasser (né en 1951) a mis au point des expériences avec l'eau, en employant des dispositifs minutieusement réglés.
Sous l'influence des vibrations, l'eau est mise en mouvement et des vaguelettes traversent sa surface. Pour certaines fréquences, les vaguelettes s'organisent en figures symétriques qui tournent lentement. On obtient aussi bien des structures polygonales que des spirales multiples dont le nombre de bras est variable, et peut prendre des valeurs aussi bien paires qu'impaires (voir article Les sons créateurs de formes).
Ces expériences nous montrent qu'il existe un rapport direct entre les formes géométriques de la matière et les fréquences sonores. Mais comment ces deux aspects sont-ils articulés? Il y a au départ la matière, la substance, qui est informe. Le son façonne la matière, il la guide pour manifester une figure géométrique. Le son est le schéma directeur de la substance. Il porte l'information structurelle.
Il est remarquable que certaines de ces formes soient analogues aux formes de la nature évoquées en début d'articles (fleurs, carapace de tortue, ..). Serait-il possible que les formes naturelles aient été produites par des sons primordiaux? C'est en tout cas ce qu'affirment de nombreuses traditions, comme nous allons le voir plus loin.
Récapitulons: Dans l'univers, les créations sont sous-tendues par des trames dont la nature est à la fois géométrique et sonore. Les contempler est pour nous un émerveillement. Mais au-delà de notre ravissement esthétique, demandons-nous si cela a un sens et quelles conséquences cela implique sur notre façon de voir le monde.
Certains avanceront que la présence de telles structures géométriques dans l'univers prouve qu'elles sont l'œuvre d'une intelligence supérieure. J'ai tendance à suivre cet argument. Mais c'est là mon intuition profonde, une certitude intime qui résonne dans mon être. Elle ne provient pas d'un raisonnement logique. C'est une autre voie de connaissance, que connaissent tous ceux qui ont vécu des expériences de conscience élargie. La connaissance acquise de cette façon est intense et pénétrante, mais elle n'est pas transmissible aux autres, sauf en les invitant à être attentifs à leur être intérieur (voir mon article Au-delà de la matière: Les plans subtils d'intelligence supérieure. Une réalité tangible et incontournable).
Restons ici dans une démarche de construction méthodique par le raisonnement. Dans ce cadre, nous ne pouvons pas invoquer l'existence d'une intelligence supérieure à ce stade de notre investigation. Par contre, nous pouvons examiner ce qu'implique le fait de désigner une forme comme étant géométrique. Selon quels critères pouvons-nous la qualifier comme telle, au-delà d'une simple sensation d'harmonie? Nous allons découvrir que la géométrie provient de la mise en œuvre de principes supérieurs.
Prenons un exemple. Un losange est manifestement reconnu comme étant une structure géométrique. Mais qu'est-ce qui nous permet de l'affirmer? C'est parce que nous reconnaissons que ses éléments sont disposés de façon particulière, selon un ordre, ou plutôt un ordonnancement. Si l'on cherche à préciser cet ordre, on découvre que les côtés d'un losange ont la même longueur et que ses diagonales se coupent à angle droit en leur milieu. Il y a des symétries, et des rapports simples entre les différentes longueurs. Le mot de géo-métrie lui même suggère une mesure (une métrique).
Autrement dit, la disposition des éléments (points, sommets, côtés, etc.) d'une forme géométrique est déterminée par une règle. Une forme est géométrique si l'on y reconnait une règle d'ordonnancement.
Il y a plusieurs façons de définir de telles règles. En voici 3 types.
Pour vous indiquer la règle d'ordonnancement d'une forme géométrique, je peux vous fournir sa formule mathématique. Pour cela, la condition est que vous compreniez le sens de cette formule, donc que vous ayez été initié au langage mathématique.
Les formules mathématiques engendrent les figures géométriques en définissant la position de chacun de leurs points. Elles fournissent donc la construction graphique de la courbe.
 |  |  |  |  |
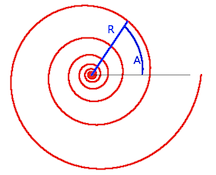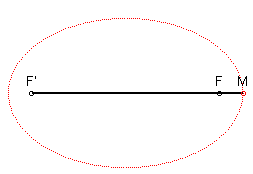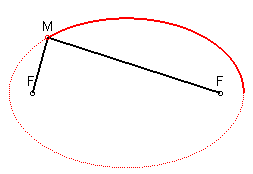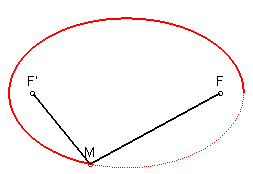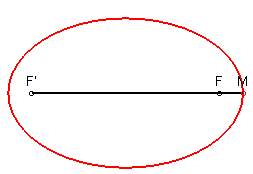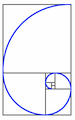| Un losange, figure géométrique faite de segments symétriques | Une spirale peut être décrite par une formule qui fournit la mesure du rayon R pour chaque angle A. Par exemple, si la formule est R=k.A on obtient une spirale d'Archimède | La lemniscate de Bernoulli | Une ellipse peut être décrite par sa formule ax2+by2=1 ou par un procédé de construction: un crayon M qui se déplace le long d'une corde tendue fixée à ses extrémités F et F'. | Spirale construite sur une trame de rectangles d'or. Elle est constituée d'une suite d'arcs de cercle de rayons croissants selon la proportion Φ=1,618. |
Les formules mathématiques décrivent des lignes et surfaces courbes. Les courbes sont une catégorie importante de figures géométriques, au même titre que les figures faites de segments droits (triangles, rectangles, polygones sur une surface plane, tétraèdres, octaèdres, cubes et autres polyèdres en volume).
Un exemple de courbe est la spirale qui, comme nous l'avons vu plus haut, est omniprésente dans les plantes, les animaux, le cosmos (voir article Spirale, mouvement de vie). Derrière la spirale visible d'une coquille d'escargot ou d'une galaxie, constituée de matière, se tient une spirale abstraite qui organise la disposition de la matière. Une spirale régulière peut être entièrement décrite par une formule mathématique. De même le cercle, les paraboles, les ellipses, les cônes, les cylindres, les cycloïdes, les lemniscates, sont des exemples de courbes qu'on peut définir par leurs formules mathématiques.
Une deuxième façon de définir une règle de géométrie est de fournir le procédé méthodique de sa construction. Une ellipse peut être définie par sa formule mathématique, mais on peut tout aussi bien la définir par un procédé graphique de construction. C'est celui d'un crayon qui se déplace le long d'une corde tendue qui prend appui sur les deux foyers de l'ellipse.
De nombreuses figures qui ne peuvent pas être définies par une formule mathématique, peuvent l'être par leur procédé de construction graphique. Un exemple est un type de spirale constitué d'une succession d'arcs de cercles dont les longueurs de rayons croissent par sauts (voir article Spirale, mouvement de vie). Le losange, de même que les polyèdres, ne sont pas engendrés par des formules mathématiques mais par des procédés de construction.
Parmi les procédés graphiques de construction, une catégorie, les fractales, revêt un aspect particulier par sa caractéristique de répétition infinie. Par définition, une figure fractale est engendrée par la répétition infinie d'un tracé graphique. Son graphisme n'est jamais terminé car il se prolonge indéfiniment. Nous avons vu plus haut des exemples de structures fractales pris dans la nature, tels que la feuille de fougère, les paysages montagneux et les superamas de galaxies.
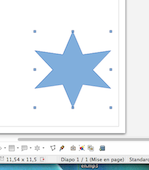
Voici à titre d'illustration un exemple de construction fractale: Tracez un carré de 3 cm de côté. Sur chacun des coins, construisez un carré 3 fois plus petit, donc de 1 cm de côté. En partant de chacun de ces quatre nouveaux petits carrés, refaites la même construction sur leurs trois côtés extérieurs en traçant des carrés 3 fois plus petits (0,33 cm). Répétez cette construction à l'infini... si possible !
Si vous effectuez ce graphisme à la main, vous comprendrez que la réduction d'échelle à chaque étape va vous limiter car les détails ajoutés sont de plus en plus fins. Mais vous pouvez parfaitement confier cette tache à un ordinateur. Vous pouvez alors lui demander d'afficher sur l'écran un zoom de plus en plus fort. Quelle que soit le type de fractale que vous dessinez, vous constaterez que ce sont les mêmes structures qui apparaissent à toutes les échelles.
 |  |  |  |
| a | b | c | |
| Exemple de construction d'une figure fractale: les 3 premières étapes (a) Un carré est orné de petits carrés 3 fois plus petits en ses coins saillants (b) chacun de ces petits carrés se voit à son tour doté en ses trois coins saillants de 3 autres carrés 3 fois plus petits (c) on recommence le processus indéfiniment, mais la limite de résolution de notre vision ne nous permet pas de distinguer les détails trop fins © A. Boudet | Construction d'une structure géométrique à l'aide d'un logiciel de dessin | ||
Pour certain types de figures fractales, une formule mathématique intervient. Mais elle ne définit pas la figure elle-même comme dans le cas des courbes. Elle définit seulement l'étape répétitive du procédé de la construction. (voir dans l'article Images fractales plusieurs types de constructions).
Nous avons appris qu'une forme est géométrique si elle est définie par une règle d'ordonnancement. Nous avons appris également que cette règle peut être donnée par une formule mathématique ou par un procédé de construction. Mais puisqu'une formule mathématique décrit elle-même une construction graphique, on peut dire que toutes les figures géométriques peuvent être engendrées par une méthode graphique.
Or qu'est-ce qu'une méthode? Ce n'est pas autre chose qu'une suite d'instructions à effectuer. C'est donc un programme de création. Nous en déduisons que toute forme géométrique peut être engendrée par un programme.
Voici un exemple de programme qui engendre une forme: imaginez que vous devez expliquer à quelqu'un au téléphone comment reproduire un dessin que vous avez sous les yeux. Vous pourrez lui dire: Prends une feuille de papier et un crayon. Pose le crayon au centre de la feuille et inscris un point. De ce point, trace une ligne verticale vers le haut sur 2 cm. Tourne de 90° à droite et trace une ligne droite horizontale de 5 cm, etc. Vous avez dicté une suite d'instructions qui a conduit à créer le dessin.
Un ordinateur est justement une machine destinée à exécuter de tels programmes et il est donc logique que la réalisation de figures géométriques soit prise en charge par des logiciels de dessins. Ces logiciels ont la capacité d'engendrer un nombre incalculable de figures des plus simples aux plus complexes et de les afficher sur l'écran de l'ordinateur.
Que se passe-t-il lorsque vous dessinez une étoile avec la souris d'un ordinateur? Votre ordinateur calcule, grâce aux commandes de votre logiciel de dessin, quels sont les points qui seront affichés sur votre écran. Tout passe par des calculs et des programmes.
De même, lorsqu'un architecte veut représenter la pièce d'une maison, il commence par dessiner un parallélépipède rectangle, puis en modifie la forme, l'habille d'une certaine texture, la représente en perspective, la fait tourner, avec des éclairages différents. Chaque fois, ce sont des calculs qui déterminent quels sont les pixels de l'écran qui doivent être allumés.
Les opérations qui consistent à représenter des objets en 3D sur un écran sont devenues familières à ceux qui utilisent un ordinateur, n'est-ce pas? Mais ont-ils réfléchi à ce que cette possibilité implique sur la nature des objets qu'ils représentent? Cela démontre que ces objets en 3 dimensions sont entièrement définis par des programmes (ou algorithmes) de création.
Les logiciels d'ordinateurs ont même la possibilité de représenter des corps humains par des programmes. Et plus encore de les animer pour en faire des films. Comment est-ce possible? Le corps humain est-il donc descriptible en terme de géométrie et de calculs?
Nous avons vu que nous pouvions discerner des géométries dans la silhouette humaine. Les procédés de réalisation de films et de vidéos d'animation poussent cette représentation un cran plus loin en finesse en modélisant le corps par un assemblage de nombreuses cellules géométriques mobiles.
Pour construire un personnage, les logiciels partent d'une représentation sous forme d'une sorte de squelette fait de fuseaux et de rotules articulés. Le squelette est ensuite habillé d'un assemblage de mailles élémentaires de forme simple telle qu'un cube, qui reconstituent la silhouette du corps. Cette grille, dite représentation en fil de fer, est une sorte d'armature fine et mobile du corps qui simule tous ses mouvements. Finalement cette armature est habillée par une texture qui lui donne une apparence humaine... ou autre. Pour faire évoluer le personnage, il suffit d'agir sur le squelette. Le résultat est vraiment étonnant. Nous pouvons nous régaler de magnifiques film d'animations comme Avatar.
Cycles de marche d'un personnage réalisés avec un logiciel d'animation 3D
Arrêtons-nous sur ce fait remarquable. Des infographistes, donc des hommes ou des femmes comme nous, savent créer des formes animées complexes de personnages humains. Les images des personnages animés sont entièrement produites par des logiciels spécialisés, qui les codent sous forme numérique. Qu'est-ce que cela nous apporte dans notre réflexion sur les codes géométriques? Cela nous montre qu'il est humainement possible de définir des silhouettes humaines et de reproduire leur mouvements uniquement par des programmes et des codes mathématiques.
Certes, par rapport à la réalité vivante, ces reproductions restent grossières, mais elles sont néanmoins réalistes. Et puisque, à leur modeste niveau, les hommes sont capables de produire des schémas directeurs numériques de l'humain avec un simple ordinateur, qu'en est-il dans les plans supérieurs de la création? Ne pouvons-nous pas imaginer que d'autres types de programmes beaucoup plus subtils pourraient être à l'origine des objets et des créatures, et guideraient leur développement? Il serait logique que ces programmes supérieurs soient bien plus puissants, et que le mode de leur encodage soit d'une complexité qui échappe encore à notre entendement.
Récapitulons: Dans l'univers, les créations sont sous-tendues par des trames géométriques et sonores. Ces trames, y compris celles de l'être humain, peuvent être régies par des programmes.
Les programmes sont inscrits à des niveaux plus abstraits. Entrons un peu plus dans la réalité de ces niveaux.
Pour comprendre l'existence de différents niveaux, revenons à la métaphore du dessinateur qui utilise un ordinateur. Nous pouvons distinguer trois plans de réalité dans le processus de ses créations:
1. Il y a d'une part la forme qui apparait sur l'écran. Elle est bien visible, donc manifestée sur le plan de nos perceptions, de nos sens.
2. Il y a d'autre part, enfoui dans les entrailles de l'ordinateur, le programme qui a engendré la forme. Le programme contient la suite des instructions. Il est véritablement le schéma directeur de la forme manifestée dans le plan le plus concret (sur l'écran).
3. Enfin, il y a l'informaticien qui a conçu le logiciel utilisé par le dessinateur, en utilisant les lois générales des langages informatiques et des mathématiques. Il l'a inventé avec sa conscience et son intelligence, donc à un niveau supérieur de réalité.
De façon analogue, nous pouvons concevoir que les formes géométriques de l'univers sont l'expression de fréquences sonores, autrement dit d'ondes vibratoires porteuses d'informations. Ces fréquences sont elles-mêmes pilotées par des programmes ou schémas directeurs qui sont inscrits à des niveaux supérieurs.
De même que la technologie de l'ordinateur impose que programmes et les géométries soient codés sous forme numérique, de même, les schémas directeurs de l'univers sont des informations codées.
Récapitulons: Les créations naturelles de l'univers sont pilotées par des schémas directeurs inscrits à des niveaux supérieurs. Ils transmettent leurs informations sous forme codée, qui se manifestent en sons et en géométries.
L'univers aurait-il donc été formé à partir de fréquences codées complexes? Si oui, c'est un scénario qui n'a rien à voir avec celui du Big Bang, pas plus qu'avec celui d'une création de tout objet et de toute créature par un dieu en 6 jours, comme on fait des pots avec de la terre.
Ce scénario nouveau met en scène une science cybernétique complexe qui régit la création des créatures et des objets, mais aussi leurs évolutions.
Les caractéristiques de cette science sont souvent esquissées dans des textes anciens, comme les textes kabbalistiques ou védiques. Ils décrivent les créations, mais aussi leurs destinées.
On trouve aussi de nombreuses références à un tel scénario dans les mythes de création du monde dans la plupart des sociétés traditionnelles et des religions. Quoique issus de cultures très éloignées les unes des autres, les mythes rapportent fréquemment que le monde a été créé par les sons, par le verbe ou par le souffle.
Pour les mayas, les dieux créent les choses en les nommant, donc en prononçant des noms. On trouve la référence au son et au souffle chez les celtes, les taoïstes chinois, les égyptiens, les Dogons au Mali, les amérindiens Navajos, Lakotas, etc. Les chrétiens apprennent que Dieu a créé le monde par son Verbe (sa parole). En outre, remarquablement, les textes anciens présentent Dieu comme un architecte, détenteur des poids et mesures de l'univers (géométrie).
Chez les hindous et les bouddhistes, le principe qui structure l'énergie primordiale est le mantra Om (ou Aum). Dans l'Asie et en Inde plus particulièrement, la tradition rapporte que dans un lointain passé, des saints hommes, les Rishis, (littéralement les clairvoyants), auraient perçu dans le silence profond de leur méditation, une série de sons traduisant les vibrations inhérentes à toute construction atomique des différents éléments de la nature. Ils donnèrent à cet ensemble de sonorités le nom de SAM-S-KR ce que nous appelons aujourd'hui le Sanskrit... Ils donnèrent à cette nouvelle langue le nom de "langage des dieux" (André Riehl, enseignant en yoga traditionnel).
Notre univers a été créé à partir de schémas directeurs qui pilotent les créations et leur évolution depuis les galaxies jusque dans l'intimité des atomes.
Dans ce contexte, l'être humain a un destin très particulier. Les informations codées qui président à son développement sont lisibles dans les champs électromagnétiques liés à l'ADN (voir article ADN électromagnétique). Mais les schémas directeurs, inscrits dans des plans plus subtils, ont subi des déviations. C'est cette histoire que j'explore dans l'article Les codes géométriques et sonores de l'Être humain. Une vision nouvelle de l'évolution. J'y montre aussi comment ces codes sont en cours de restauration, ce qui donne un sens optimiste aux bouleversements que traverse l'humanité.
Les chimistes étudient les propriétés chimiques ou physico-chimiques des différentes substances. Ils les comparent et tentent de comprendre les causes de leurs similitudes et de leurs différences. Par exemple, ils mesurent les températures de fusion et d'ébullition des corps simples. Ou encore leur volume atomique (volume occupé par 1g ou 1 kg de l'élément). Ils prennent des mesures magnétiques ou électriques, comme celles de l'énergie d'ionisation, qui est la tension électrique nécessaire pour ioniser un atome en lui arrachant un électron.
C'est d'abord en étudiant les diverses substances qui composent les minéraux, les poudres, les liquides et les gaz présents sur la Terre, que les chimistes ont compris qu'elles étaient constituées de la combinaison d'un petit nombre de corps simples (moins de 100). On sait maintenant qu'un corps (ou élément) simple (par exemple le fer) est un assemblage d'atomes identiques, contrairement aux corps composés (comme le sel de cuisine) composés d'atomes différents (le sel est composé de sodium et de chlore). Aux 18e et 19e siècles, les chimistes ignoraient encore la constitution de la matière mais constataient qu'au cours des réactions chimiques les corps se combinaient dans des proportions parfaitement définies. Ils comprirent que les combinaisons impliquaient des quantités qui étaient des multiples d'une masse unité spécifique à chaque élément. On comprendra plus tard qu'il s'agissait de la masse d'un atome. Chaque élément est caractérisé par sa masse atomique (on disait alors son poids atomique). En 1858, le chimiste italien Stanislao Cannizzaro (1826 - 1910) parvint à déterminer la valeur de ces masses atomiques.
Ensuite, les chimistes se sont aperçus que les masses atomiques de tous les éléments étaient approximativement multiples de la masse atomique de l'hydrogène. En attribuant la masse 1 à l'hydrogène, on trouve les masses 12 pour le carbone, 14 pour l'azote, 16 pour l'oxygène, 32 pour le soufre, etc. Par la suite, sachant que la masse d'un atome est concentrée dans son noyau, et que le noyau est fait d'un nombre déterminé de protons et de neutrons dont les masses sont très voisines, on comprit que la masse 1 de l'hydrogène correspond à un seul nucléon (un proton). Il devint alors évident que la masse atomique (notée A) est égale au nombre de nucléons. Par exemple l'atome de carbone, de masse A=12, contient 6 protons et 6 neutrons.
Les chimistes se demandèrent comment les valeurs des propriétés chimiques ou physico-chimiques des éléments dépendaient de leur masse atomique. Ils reportèrent donc les valeurs mesurées dans des tableaux ou graphiques où les éléments sont classés par masses atomiques croissantes. Ils s'aperçurent avec étonnement que les valeurs des propriétés physico-chimiques n'augmentent pas de façon continue ni ne diminuent pour des éléments de masse atomique croissante. Elles affichent des périodicités bien visibles.
 |  |
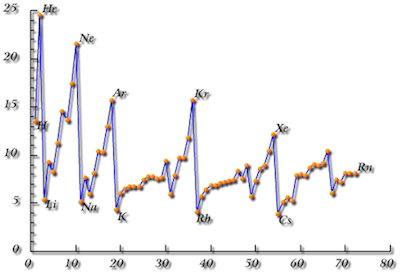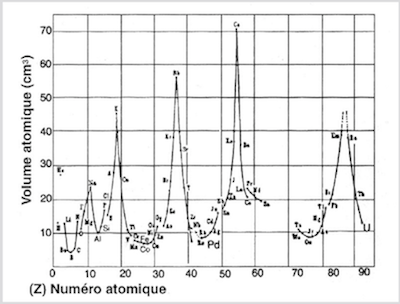| Énergie d'ionisation des éléments en fonction de leur numéro atomique. Les minimums correspondent aux éléments de la première colonne (alcalins). Les maximums correspondent à la dernière colonne (gaz rares). Source: Les atomes polyélectroniques, Ulysse, Ingénierie Multimédia de Formations, Université Bordeaux 1, 1999 | Volume atomique des éléments en fonction de leur numéro atomique (cm3 par mole). Les maximums correspondent aux éléments du groupe de la première colonne (alcalins), situés au début de chaque ligne. Les mimimums (Z = 8, 14, 26 et 46 - O, Si, Fe, Pd) correspondent presque exactement, dans le modèle de Moon, aux éléments pour lesquels les sommets des polyèdres nucléaires sont complètement occupés. Source: Atomic Structure and Spectral Lines, Arnold Sommerfeld, Methuen & Co. Ltd. 1923, fig.24 p.98, cité par Laurence Hecht, revue Fusion n°84, 2001 |
L'existence de ces périodicités ou cycles a incité plusieurs savants à classer les éléments par périodes. L'un des premiers fut le chimiste allemand Lothar Meyer (1830 - 1895) qui a élaboré une version rudimentaire des périodicités en considérant la variation du volume atomique en fonction de la masse atomique (pas encore le numéro atomique). La classification périodique proposée en 1869 par le chimiste russe Dmitri Mendeleïev (1834 - 1907) est plus connue. Il dispose les éléments en plusieurs lignes, changeant de ligne à chaque retour d'une propriété. Les éléments qui présentent des propriétés semblables se retrouvent sur une même colonne.
Nous venons donc de mettre en évidence l'existence de cycles, c'est-à-dire des répétitions périodiques, dans les atomes.
Les cycles ont été mis en évidence par leurs effets physiques extérieurs. Cela correspond-il à une structure interne particulière des atomes? Oui, comme nous allons le voir.
Chimiquement, un élément est défini par le nombre Z de ses protons, appelé numéro
atomique. Par exemple tous les atomes qui ont 6 protons (Z=6) sont du carbone. Les neutrons s'ajoutent aux protons pour contribuer à la masse, de sorte que le total des nucléons est A. On note cet élément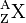 
où X représente son nom. Par exemple, le carbone est noté 
.
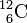Mais pour un même élément chimique de numéro atomique Z défini (par exemple le carbone Z=6), on peut trouver plusieurs types d'atomes qui diffèrent par le nombre de neutrons, donc par leur masse atomique A. Cette découverte a été faite en 1912 par le physicien anglais Joseph John Thomson (1856 - 1940), le même qui avait découvert l'électron (voir article Matière et rayonnements). Il constata que les ions du néon (Z=10), propulsés dans un champ électrique et un champ magnétique, n'étaient pas tous déviés de la même façon, mais selon deux angles différents, ce qui indiquait qu'ils avaient des masses différentes.
En effet, il existe un néon de masse atomique 20 et un autre de masse 22. C'est ce qu'on appelle des isotopes. Des isotopes sont des atomes qui ont le même nombre de protons, mais différent par le nombre de neutrons et donc par leur masse atomique A. Le carbone 12, noté 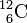, et le carbone 14, noté 
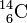, sont des isotopes de l'élément carbone.
À la suite de la découverte des isotopes et du numéro atomique, la classification périodique subit une évolution. On s'aperçut que la variation des propriétés chimiques des éléments dépendait, non pas de leur masse atomique A, mais précisément de leur numéro atomique Z. En les classant en fonction de Z, on supprimait certaines incohérences. Dans cette nouvelle classification, les cycles - les retours à la ligne du tableau - sont reliés au numéro atomique (nombre Z de ses protons).
Le nombre Z de protons est aussi le nombre d'électrons présents dans le cortège électronique. On démontra que les cycles des éléments sont l'expression de la structure en couche des orbitales des électrons.
En effet, lorsqu'on soumet un gaz à des décharges électriques, il émet des fréquences lumineuses qui sont provoquées par le passage des électrons d'une orbitale à l'autre. Des expériences effectuées à partir de 1885 ont montré que les fréquences lumineuses sont dénombrables et déterminées par une règle liée à de petits nombres entiers 1, 2, 3, etc. Selon la physique quantique, cela implique que les électrons sont confinés dans des couches qui ne peuvent recevoir chacune qu'un nombre maximum bien déterminé d'électrons. C'est comme si elles étaient constituées de cases en nombre déterminé qui peuvent contenir chacune un seul électron.
Ainsi, la première couche comporte deux cases. Dans l'atome d'hydrogène, seule la première case est occupée par un électron. Corrélativement, le noyau contient un seul proton. Si les deux cases sont occupées, on a deux électrons dans la couche et deux protons dans le noyau, et il s'agit de l'hélium. Avec lui, la couche est pleine.
Lorsque le nombre de protons et d'électrons augmente, les électrons se disposent progressivement sur la couche suivante, avec 8 cases distribuées en deux sous-couches de 2 et 6 électrons. Cela nous conduit de l'élément lithium (Z=3) à l'élément néon (Z=10). La troisième période a également 8 cases (Z=11 à 18). La 4e ligne comporte 18 cases, réparties en 3 sous-couches de 2, 6 et 10 cases (Z=19 à 36). Et ainsi de suite.
Qu'est-ce que cela signifie sur le plan de l'ordre géométrique? Que les atomes sont construits selon des cycles (sous-couches) de 2, de 6, de 10 et de 14, qui s'additionnent en cycles (couches) de 2, de 8, de 18 et de 32.
Puisque le nombre de protons dans le noyau est le même que celui des électrons dans le cortège d'orbitales, comment les cycles que nous venons de mettre en évidence dans les orbitales se répercutent-ils sur les protons? Subissent-ils eux aussi des sauts pour les mêmes nombres? Il est difficile de le dire, car il est beaucoup plus difficile de faire réagir les protons que les électrons. On l'a vu, il suffit d'envoyer des rayonnements adéquats sur les électrons pour qu'ils changent d'orbitales et se manifestent. Par contre, toucher au noyau revient à provoquer des réactions nucléaires, comme son nom l'indique (latin nucleus, noyau). C'est délicat.
Toutefois, à partir de diverses observations de réactions nucléaires telles que la désintégration radioactive, ou encore les fissions nucléaires, les physiciens ont élaboré des modèles de structure du noyau. Celui qui reçoit les faveurs actuelles des scientifiques est justement structuré en couches. Il a été principalement développé par la physicienne étasunienne Maria Goeppert Mayer (1906 - 1972) en 1949. Les couches dont il est question ne sont pas localisées dans l'espace, elles sont identifiées par leurs manifestations. Ces manifestations changent de façon brusque lorsque le nombre de nucléons atteint certaines valeurs que la physicienne a nommées nombres magiques et qui correspondent au remplissage successif de 8 couches. Ce sont les nombres 2, 8, 20, 28, 50, 82, 126 et 184.
en anglais
Texte conforme à la nouvelle orthographe française (1990)
16 novembre 2014
